Note ≡ 넘파이를 사용한 고윳값 분해

numpy.linalg.eig 함수는 대칭과 비대칭 정방 행렬(square matrix)을 모두 다룰 수 있지만 이따금 복소수 고윳값을 반환합니다.

이와 비슷하게 에르미트 행렬(Hermetian matrix)⁵을 분해하기 위해 구현된 numpy.linalg.eigh 함수는 공분산 행렬과 같은 대칭 행렬을 다룰 때 수치적으로 더 안정된 결과를 만듭니다. 즉, numpy.linalg.eigh는 항상 실수 고윳값을 반환합니다.

Note ≡

역주 사이킷런의 PCA 클래스는 직접 고윳값과 고유 벡터를 계산하는 대신 특이 값 분해(singular value decomposition) 방식을 사용하여 주성분을 구합니다. 원점에 중앙이 맞추어진 공분산 행렬을 특이 값 분해로 표현하면 다음과 같습니다.

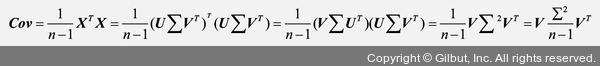
따라서 V 가 공분산 행렬의 고유 벡터이고 주성분이 됩니다. 사이킷런의 PCA는 scipy.linalg.svd 함수를 사용하여 주성분 V를 구합니다. 이 식에서 ∑는 공분산 행렬이 아니라 행렬 X와 같은 크기의 대각 행렬을 나타냅니다.

공식에서 볼 수 있듯이 고윳값은 특이 값 ∑를 제곱하여 (샘플 개수 - 1)로 나누어 계산할 수 있습니다. 사이킷런은 (샘플 개수 - 1)이 아닌 샘플 개수로 나누는 버그를 가지고 있었습니다. 사이킷런 0.19 버전에서 (샘플 개수 - 1)로 수정되었고 특이 값을 저장하는 singular_values_ 속성도 추가되었습니다.