결과 그래프는 첫 번째 주성분이 거의 분산의 40%를 커버하고 있음을 보여 줍니다.
또 처음 두 개의 주성분이 데이터셋에 있는 분산의 대략 60%를 설명합니다.
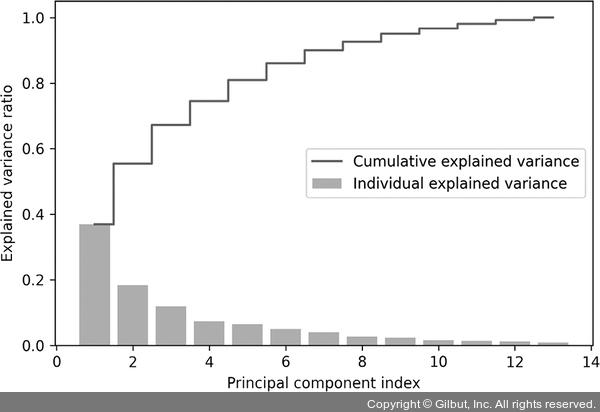
▲ 그림 5-2 주성분의 설명된 분산
설명된 분산 그래프가 4장에서 랜덤 포레스트로 계산한 특성 중요도를 떠올리게 하지만 PCA는 비지도 학습이란 점을 기억하세요. 클래스 레이블에 관한 정보는 사용하지 않았습니다. 랜덤 포레스트는 클래스 소속 정보를 사용하여 노드의 불순도를 계산하는 반면,6 분산은 특성 축을 따라 값들이 퍼진 정도를 측정합니다.
6 역주 결정 트리의 특성 중요도는 노드에 사용된 특성별로 (부모 노드의 샘플 비율 × 불순도) - (왼쪽 자식 노드의 샘플 비율 × 불순도) - (오른쪽 자식 노드의 샘플 비율 × 불순도)를 계산하여 더하고, 특성 중요도의 합이 1이 되도록 정규화한 것입니다. 여기서 샘플 비율은 전체 샘플 개수에 대한 비율입니다. 랜덤 포레스트의 특성 중요도는 각 결정 트리 특성 중요도의 합을 트리 개수로 나눈 것입니다.