Note ≡ 거울 투영(mirrored projection)
사용하는 넘파이와 LAPACK 버전에 따라 부호가 반대인 행렬 W를 얻을 수 있습니다. 이는 문제가 아닙니다. 만약 v가 행렬 ∑의 고유 벡터이면 다음과 같습니다.
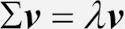
여기서 v는 고유 벡터이고 -v 또한 고유 벡터입니다. 다음과 같이 기초대수학을 사용하면 방정식의 양쪽에 α를 곱할 수 있습니다.
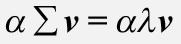
행렬 곱셈은 스칼라 곱셈에 대해 결합법칙이 성립하므로 다음과 같이 다시 정렬할 수 있습니다.
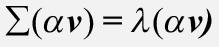
이렇게 쓰면 αv는 α = 1과 α = -1일 때 같은 고윳값 λ를 갖는 고유 벡터임을 알 수 있습니다.
투영 행렬을 사용하면 샘플 x(13차원의 행 벡터)를 PCA 부분 공간(두 개의 주성분)을 투영하여 x'를 얻을 수 있습니다. 두 개의 특성으로 구성된 2차원 샘플 벡터입니다.
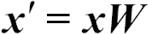
>>> X_train_std[0].dot(w)
array([ 2.38299011, 0.45458499])
비슷하게 전체 124×13 차원의 훈련 데이터셋을 행렬 점곱으로 두 개의 주성분에 투영할 수 있습니다.

>>> X_train_pca = X_train_std.dot(w)