개별 산포 행렬 Si를 산포 행렬 SW로 모두 더하기 전에 스케일을 조정해야 합니다. 산포 행렬을 클래스 샘플 개수 ni로 나누면 사실 산포 행렬을 계산하는 것이 공분산 행렬 ∑i를 계산하는 것과 같아집니다. 즉, 공분산 행렬은 산포 행렬의 정규화 버전입니다.
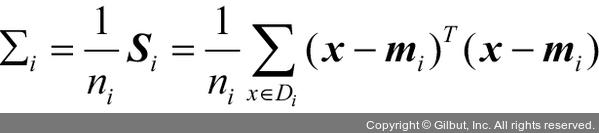
>>> d = 13 # 특성 개수
>>> S_W = np.zeros((d, d))
>>> for label, mv in zip(range(1, 4), mean_vecs):
... class_scatter = np.cov(X_train_std[y_train==label].T)
... S_W += class_scatter
>>> print('스케일 조정된 클래스 내의 산포 행렬: %sx%s'
... % (S_W.shape[0], S_W.shape[1]))
스케일 조정된 클래스 내의 산포 행렬: 13x13
클래스 내 산포 행렬(또는 공분산 행렬)을 계산한 후 다음 단계로 넘어가 클래스 간의 산포 행렬 SB를 계산하겠습니다.
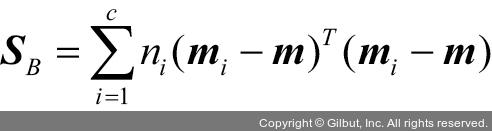
여기서 m은 모든 클래스의 샘플을 포함하여 계산된 전체 평균입니다.
>>> mean_overall = np.mean(X_train_std, axis=0)
>>> mean_overall = mean_overall.reshape(d, 1) # 열 벡터로 만들기
>>> d = 13 # 특성 개수
>>> S_B = np.zeros((d, d))
>>> for i, mean_vec in enumerate(mean_vecs):
... n = X_train[y_train == i + 1, :].shape[0]
... mean_vec = mean_vec.reshape(d, 1) # 열 벡터로 만들기
... S_B += n * (mean_vec - mean_overall).dot(
... (mean_vec - mean_overall).T)
>>> print('클래스 간의 산포 행렬: %sx%s' % (
... S_B.shape[0], S_B.shape[1]))
클래스 간의 산포 행렬: 13x13