Note ≡

역주 이전 절에서 단계별로 설명한 LDA 구현은 LinearDiscriminantAnalysis 클래스의 solver 매개변수가 'eigen'일 때입니다. 실제 사이킷런의 LDA 구현은 책과는 조금 다릅니다.

전체 평균과 클래스별 평균 사이의 관계는 다음과 같습니다.

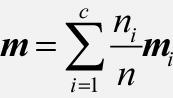
이를 클래스 내 산포 행렬 S_W에 적용하고 클래스별 산포 행렬 S_i를 클래스별 공분산 행렬 ∑_i로 정의하면 다음과 같이 쓸 수 있습니다.

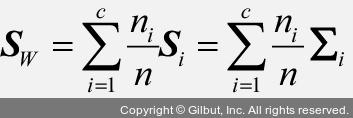
먼저 클래스 비율을 계산하고 그다음 클래스 내 산포 행렬 S_W를 계산해 보죠.

>>> y_uniq, y_count = np.unique(y_train, return_counts=True)
>>> priors = y_count / X_train_std.shape[0]
>>> priors
array([0.3306, 0.4032, 0.2661])

>>> s_w = np.zeros((X_train_std.shape[1], X_train_std.shape[1]))
>>> for i, label in enumerate(y_uniq):
>>>     s_w += priors[i] * np.cov(X_train_std[y_train == label].T, bias: True)

앞 코드에서 np.cov() 함수를 사용할 때 bias 매개변수를 True로 지정했습니다. 기본적으로 np.cov() 함수는 공분산 행렬을 계산할 때 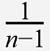을 곱합니다. 사이킷런 구현을 따라 bias = True로 설정하면 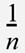을 곱하도록 바꿀 수 있습니다.

클래스 간의 산포 행렬도 클래스 비율을 곱해 계산합니다.

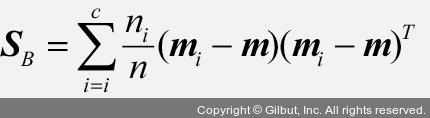
s_b = np.zeros((X_train_std.shape[1], X_train_std.shape[1]))
for i, mean_vec in enumerate(mean_vecs):
    n = X_train_std[y_train == i + 1].shape[0]
    mean_vec = mean_vec.reshape(-1, 1)
    s_b += priors[i] * (mean_vec - mean_overall).dot((mean_vec - mean_overall).T)

S_W^-1S_B를 직접 구해 고윳값 분해를 하는 대신 scipy.linalg.eigh 함수에 S_B와 S_W를 전달하면 S_Bw = λS_Ww 식의 고윳값을 바로 계산할 수 있습니다. 계산 후에 고윳값 크기의 역순으로 고유 벡터를 정렬하여 최종 고유 벡터를 구합니다.

import scipy
ei_val, ei_vec = scipy.linalg.eigh(s_b, s_w)
ei_vec = ei_vec[:, np.argsort(ei_val)[::-1]]

여기서 계산한 것과 LinearDiscriminantAnalysis 클래스의 결과와 같은지 확인해 보죠. 이 데이터셋의 클래스는 세 개이기 때문에 n_components를 설정하지 않아도 자동으로 두 개의 고유 벡터만 사용합니다.

lda_eigen = LDA(solver='eigen')
lda_eigen.fit(X_train_std, y_train)

클래스 내 산포 행렬은 lda_eigen 객체의 covariance_ 속성에 저장되어 있습니다.

>>> np.allclose(s_w, lda_eigen.covariance_)
True

클래스 간의 산포 행렬은 따로 제공되지는 않지만 총 산포 행렬(total scatter matrix) S_T에서 클래스 내 산포 행렬 S_W를 빼서 구할 수 있습니다.

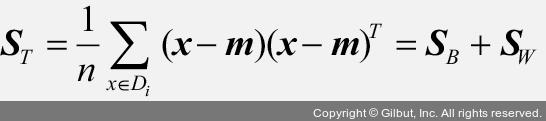
>>> Sb = np.cov(X_train_std.T, bias=True) - lda_eigen.covariance_
>>> np.allclose(Sb, s_b)
True

구해진 고유 벡터는 scalings_ 속성에 저장되어 있습니다. 클래스가 세 개이므로 두 개의 고유 벡터(선형 판별 벡터)를 비교해 봅니다.

>>> np.allclose(lda_eigen.scalings_[:, :2], ei_vec[:, :2])
True

transform 메서드는 단순히 샘플과 고유 벡터의 점곱으로 구현할 수 있습니다.

>>> np.allclose(lda_eigen.transform(X_test_std), np.dot(X_test_std, ei_vec[:, :2]))
True

LinearDiscriminantAnalysis 클래스의 solver 매개변수 기본값은 'svd'로 특이 값 분해를 사용합니다. 산포 행렬을 직접 계산하지 않기 때문에 특성이 많은 데이터셋에도 잘 작동합니다.