5.3.1 커널 함수와 커널 트릭

3장에서 커널 SVM에 관해 배운 것을 떠올려 보면 비선형 문제를 해결하기 위해 클래스가 선형으로 구분되는 새로운 고차원 특성 공간으로 투영할 수 있습니다. k 고차원 부분 공간에 있는 샘플 를 정의합니다.

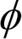함수를 d 차원의 원본 데이터셋에서 더 큰 k 차원의 특성 공간으로 매핑하기 위해 원본 특성의 비선형 조합을 만드는 함수로 생각할 수 있습니다.

예를 들어 2차원(d = 2)의 특성 벡터 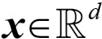가 있으면(x는 d개의 특성으로 구성된 열 벡터), 매핑 가능한 3D 공간은 다음과 같습니다.

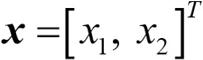
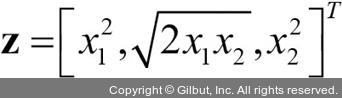
다른 말로 하면 커널 PCA를 통한 비선형 매핑을 수행하여 데이터를 고차원 공간으로 변환합니다. 그다음 고차원 공간에 표준 PCA를 사용하여 샘플이 선형 분류기로 구분될 수 있는 저차원 공간으로 데이터를 투영합니다(샘플이 이 입력 공간에서 잘 구분될 수 있다고 가정합니다). 이 방식의 단점은 계산 비용이 매우 비싸다는 것입니다. 여기에 커널 트릭(kernel trick)이 등장합니다. 커널 트릭을 사용하면 원본 특성 공간에서 두 고차원 특성 벡터의 유사도를 계산할 수 있습니다.

계산 비용이 비싼 문제를 해결하는 커널 트릭에 대해 자세히 알아보기 전에 이 장 서두에서 구현한 표준 PCA 방식을 다시 생각해 보죠. 두 개의 특성 k와 j 사이의 공분산은 다음과 같이 계산합니다.