μ_j = 0, μ_k = 0처럼 특성 평균을 0에 맞추었으므로 이 식은 다음과 같이 간단히 쓸 수 있습니다.

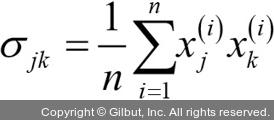
이 식은 두 특성 간의 공분산을 의미합니다. 공분산 행렬 ∑를 계산하는 일반식으로 써 봅시다.

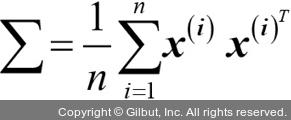
베른하르트 슐코프(Bernhard Scholkopf)는 이 방식을 일반화하여 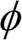를 통한 비선형 특성 조합으로 원본 특성 공간의 샘플 사이의 점곱을 대체했습니다.¹³

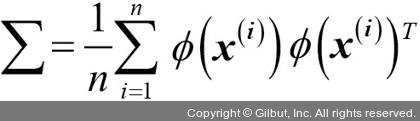
이 공분산 행렬에서 고유 벡터(주성분)를 얻기 위해서는 다음 식을 풀어야 합니다.

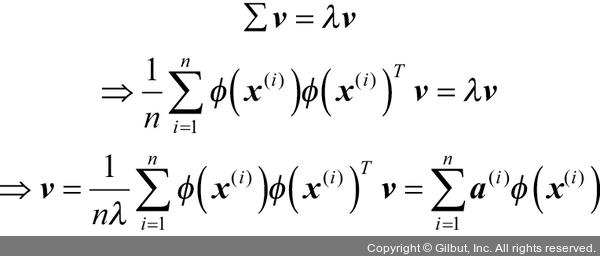
여기서 λ와 v는 공분산 행렬 ∑의 고윳값과 고유 벡터입니다. a는 커널 (유사도) 행렬 K의 고유 벡터를 추출함으로써 구할 수 있습니다. 다음 노트에서 이를 알아보겠습니다.