적절한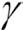 
값을 주고 RBF 커널 PCA 구현을 사용해 보겠습니다.
>>> X_kpca = rbf_kernel_pca(X, gamma=15, n_components=2)
>>> fig, ax = plt.subplots(nrows=1, ncols=2, figsize=(7,3))
>>> ax[0].scatter(X_kpca[y==0, 0], X_kpca[y==0, 1],
... color='red', marker='^', alpha=0.5)
>>> ax[0].scatter(X_kpca[y==1, 0], X_kpca[y==1, 1],
... color='blue', marker='o', alpha=0.5)
>>> ax[1].scatter(X_kpca[y==0, 0], np.zeros((500,1))+0.02,
... color='red', marker='^', alpha=0.5)
>>> ax[1].scatter(X_kpca[y==1, 0], np.zeros((500,1))-0.02,
... color='blue', marker='o', alpha=0.5)
>>> ax[0].set_xlabel('PC1')
>>> ax[0].set_ylabel('PC2')
>>> ax[1].set_ylim([-1, 1])
>>> ax[1].set_yticks([])
>>> ax[1].set_xlabel('PC1')
>>> plt.tight_layout()
>>> plt.show()
RBF 커널 PCA가 두 클래스를 선형적으로 구분할 수 있는 새로운 부분 공간으로 데이터를 투영했습니다.
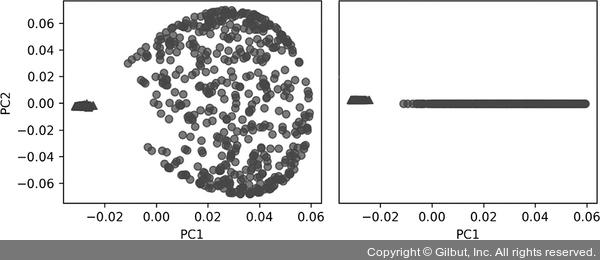
▲ 그림 5-17 커널 PCA를 적용한 동심원 데이터셋