Note ≡ 매니폴드 학습(manifold learning)

사이킷런 라이브러리는 비선형 차원 축소를 위한 고급 기법을 구현해 놓았습니다. 이들은 책 범위를 넘어섭니다. 관심 있는 독자는 사이킷런의 구현에 대한 소개와 이해를 돕는 예제를 온라인 문서에서 읽을 수 있습니다(http://scikit-learn.org/stable/modules/manifold.html).

Note ≡

역주 사이킷런의 매니폴드(manifold) 알고리즘을 반달 모양 데이터셋과 동심원 데이터셋에 적용해 보겠습니다. 먼저 변환된 2차원 데이터셋을 그래프로 그리기 위한 간단한 함수를 정의합니다.

>>> def plot_manifold(X, y):
...     plt.scatter(X[y == 0, 0], X[y == 0, 1],
...                 color='red', marker='^', alpha=0.5)
...     plt.scatter(X[y == 1, 0], X[y == 1, 1],
...                 color='blue', marker='o', alpha=0.5)
...     plt.xlabel('PC1')
...     plt.ylabel('PC2')
...     plt.tight_layout()
...     plt.show()

지역 선형 임베딩(Locally Linear Embedding, LLE)은 이웃한 샘플 간의 거리를 유지하는 저차원 투영을 찾습니다. 지역 선형 임베딩을 구현한 사이킷런의 LocallyLinearEmbedding 클래스를 앞에서 적재한 반달 모양 데이터셋에 적용해 보겠습니다.

>>> from sklearn.manifold import LocallyLinearEmbedding
>>> lle = LocallyLinearEmbedding(n_components=2, random_state=1)
>>> X_lle = lle.fit_transform(X)
>>> plot_manifold(X_lle, y)

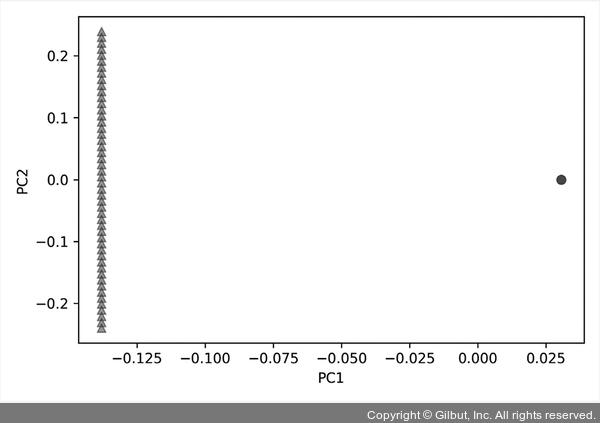
▲ 그림 5-20 지역 선형 임베딩을 적용한 반달 데이터셋

반달 모양은 유지되지 않았지만 두 클래스가 뚜렷하게 구분되었습니다. 그다음 같은 데이터에 t-SNE 알고리즘을 적용해 보겠습니다.

t-SNE(t-distributed Stochastic Neighbor Embedding)는 데이터 포인트 간의 유사도를 결합 확률( joint probability)로 변환하고, 저차원과 고차원의 확률 사이에서 쿨백-라이블러(Kullback-Leibler) 발산을 최소화합니다. t-SNE는 특히 고차원 데이터셋을 시각화하는 성능이 뛰어납니다. 사이킷런에는 TSNE 클래스에 구현되어 있습니다.

>>> from sklearn.manifold import TSNE
>>> tsne = TSNE(n_components=2, random_state=1)
>>> X_tsne = tsne.fit_transform(X)
>>> plot_manifold(X_tsne, y)

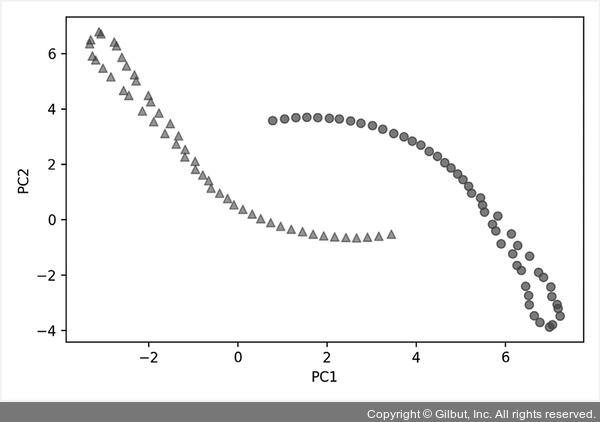
▲ 그림 5-21 t-SNE를 적용한 반달 데이터셋

t-SNE는 두 클래스를 선형적으로 구분할 수 있을 정도로 잘 분리했고 원래 반달 모양도 어느 정도 유지하고 있는 것을 볼 수 있습니다.

이번에는 KernelPCA, LocallyLinearEmbedding, TSNE를 동심원 데이터셋에 적용해 보겠습니다. 먼저 동심원 데이터셋을 다시 생성하고 KernelPCA를 적용합니다.

>>> from sklearn.datasets import make_circles
>>> X, y = make_circles(n_samples=1000, random_state=123, noise=0.1, factor=0.2)
>>> scikit_kpca = KernelPCA(n_components=2, kernel='rbf', gamma=15)
>>> X_skernpca = scikit_kpca.fit_transform(X)
>>> plot_manifold(X_skernpca, y)

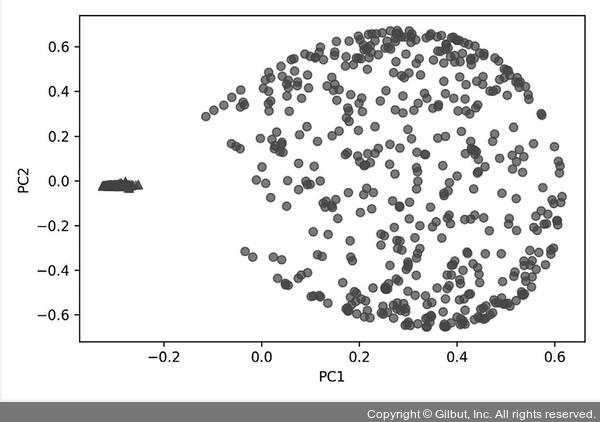
▲ 그림 5-22 KernelPCA를 적용한 동심원 데이터셋

앞서 직접 구현한 rbf_kernel_pca 함수와 거의 같은 결과를 볼 수 있습니다. 이번에는 LocallyLinear Embedding 클래스에 적용해 보겠습니다.

>>> from sklearn.manifold import LocallyLinearEmbedding
>>> lle = LocallyLinearEmbedding(n_components=2, random_state=1)
>>> X_lle = lle.fit_transform(X)
>>> plot_manifold(X_lle, y)

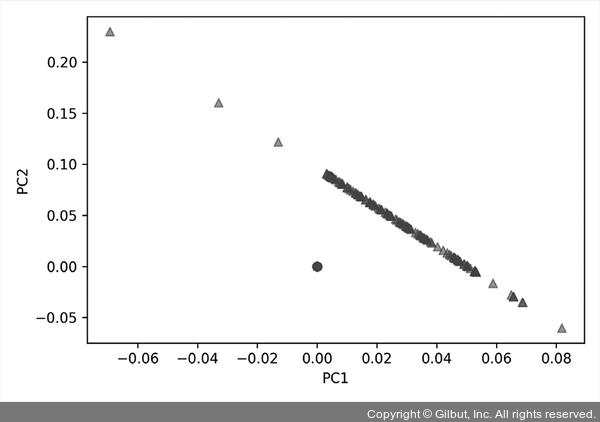
▲ 그림 5-23 지역 선형 임베딩을 적용한 동심원 데이터셋

결과 그래프를 보면 역시 두 클래스를 선형적으로 뚜렷하게 구분할 수 있습니다. 마지막으로 t-SNE에 적용해 보죠.

>>> from sklearn.manifold import TSNE
>>> tsne = TSNE(n_components=2, random_state=1)
>>> X_tsne = tsne.fit_transform(X)
>>> plot_manifold(X_tsne, y)

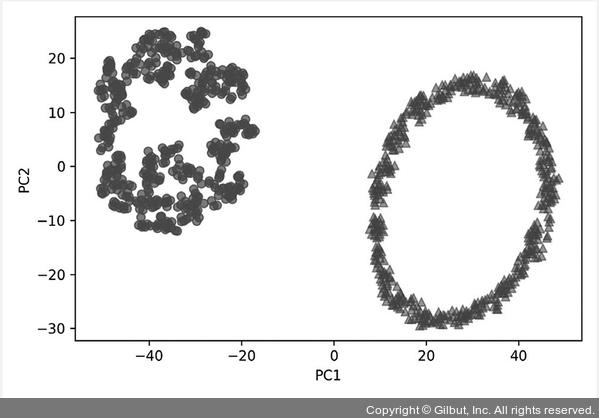
▲ 그림 5-24 t-SNE를 적용한 동심원 데이터셋

t-SNE의 결과는 놀랍습니다. 두 동심원을 선형적으로 완벽하게 분리했을 뿐만 아니라 동심원의 모양도 거의 보존하고 있습니다.