이전 코드에서 자주 보았던 사이킷런의 StratifiedKFold를 사용했습니다. 각 반복에서 sklearn.metrics 모듈의 roc_curve 함수를 사용하여 pipe_lr 파이프라인에 있는 LogisticRegression 모델의 ROC 값을 계산했습니다. 또 사이파이(SciPy)의 interp 함수를 사용하여 세 개의 폴드에 대한 ROC 곡선을 보간하여 평균을 구했습니다. 그다음 auc 함수를 사용하여 곡선 아래 면적을 계산합니다. 만들어진 ROC 곡선을 보면 폴드에 따라 어느 정도 분산이 있음을 알 수 있습니다. 평균 ROC AUC(0.76)는 완벽한 경우(1.0)와 랜덤 추측(0.5)¹⁸ 사이에 있습니다.

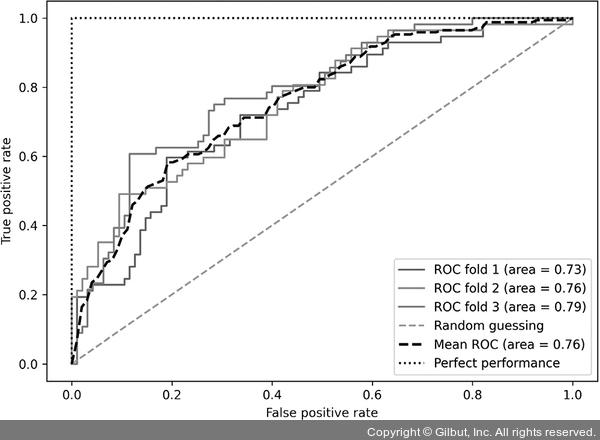
▲ 그림 6-13 ROC 곡선

ROC AUC 점수에만 관심이 있다면 sklearn.metrics 모듈의 roc_auc_score 함수를 사용할 수도 있습니다. 비슷하게 이 모듈에는 이전 절에서 소개했던 다른 측정 함수(예를 들어 precision_score)가 포함되어 있습니다.

ROC AUC로 분류 모델의 성능을 조사하면 불균형한 데이터셋에서 분류기의 성능에 대해 더 많은 통찰을 얻을 수 있습니다. 정확도를 ROC 곡선 하나의 구분점으로 해석할 수 있지만 브래들리(A. P. Bradley)는 ROC AUC와 정확도가 대부분 서로 비례한다는 것을 보였습니다.¹⁹