예를 들어 class1 = -1이고 class2 = +1인 이진 분류 작업에서 과반수 투표 예측은 다음과 같이 쓸 수 있습니다.
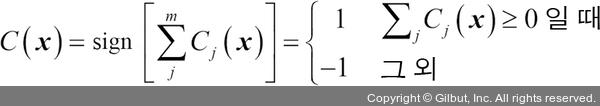
앙상블 방법이 개별 분류기보다 성능이 뛰어난 이유를 설명하기 위해 간단한 조합 이론을 적용해 보겠습니다. 다음 예에서 이진 분류 작업에 대해 동일한 에러율(error rate) ε을 가진 n개의 분류기를 가정해 보죠. 또한, 모든 분류기는 독립적이고 발생하는 오차는 서로 상관관계가 없다고 가정합니다. 이런 가정하에 이 분류기의 앙상블이 만드는 오차 확률을 이항 분포(binomial distribution)의 확률 질량 함수(probability mass function)로 표현할 수 있습니다.
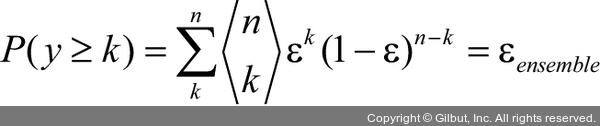
여기서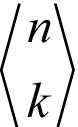 
는 이항 계수(binomial coefficient)로 n개의 원소에서 k개를 뽑는 조합의 가짓수입니다. 이 식은 앙상블의 예측이 틀릴 확률을 계산합니다. 좀 더 구체적으로 예를 들어 보죠. 에러율이 0.25(ε = 0.25)인 분류기 11개(n = 11)로 구성된 앙상블의 에러율은 다음과 같습니다.2
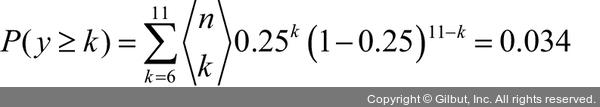
Note ≡ 이항 계수
이항 계수는 크기가 n인 집합에서 순서를 고려하지 않고 k개의 부분 집합을 선택할 수 있는 방법을 나타냅니다. 종종 ‘n choose k’라고 읽습니다. 순서에 상관하지 않기 때문에 이항 계수는 조합 또는 조합의 가짓수라고 말하기도 합니다. 수식으로 표현하면 다음과 같습니다.
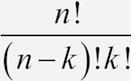
여기서 ! 기호는 팩토리얼(factorial)을 나타냅니다. 예를 들어 3! = 3×2×1 = 6입니다.
2 역주 실패할 확률이 25%일 때 11개의 분류기로 구성된 앙상블이 실패하려면 여섯 개 이상이 실패해야 합니다. 11개의 분류기에서 실패할 여섯개를 조합할 수 있는 가짓수는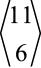 
입니다. 결국 여섯 개의 분류기가 실패할 확률은 
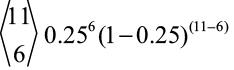이 됩니다. 이런 방식으로 11개가 모두 실패할 경우까지 확률을 더합니다.