가중치 계산 공식이 처음에는 조금 복잡해 보일 수 있으므로 단계별로 계산을 수행해 보겠습니다. 단계 2-c에 나와 있는 가중치된 에러율 ε을 먼저 계산해 보죠.

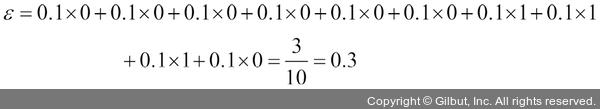
그다음 단계 2-d에 나오는 학습기 가중치 α_j를 계산합니다. 나중에 단계 2-e에서 가중치를 업데이트할 때와 단계 3에서 다수결 투표 예측을 위한 가중치에 사용됩니다.

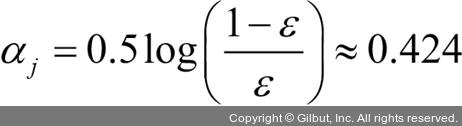
학습기 가중치 α_j를 계산한 후 다음 식을 사용하여 가중치 벡터를 업데이트할 수 있습니다.

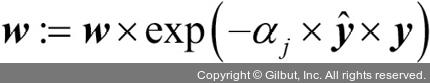
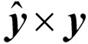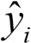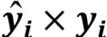여기서 는 예측 클래스 레이블 벡터와 진짜 클래스 레이블 벡터 사이의 원소별 곱셈입니다. 예측 가 맞으면 는 양의 값이 되고 α_j도 양의 값이기 때문에 i번째 가중치가 감소합니다.²¹

비슷하게 예측 레이블 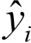가 맞지 않으면 i번째 가중치가 다음과 같이 증가합니다.

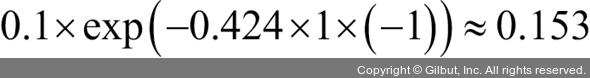
또는 다음과 같습니다.

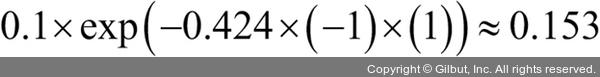
가중치 벡터의 각 가중치를 업데이트하고 난 후 가중치의 합이 1이 되도록 정규화합니다(단계 2-f).

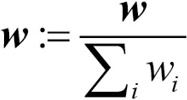
여기서 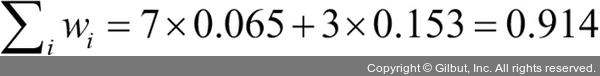입니다.

옳게 분류된 샘플에 대응하는 가중치는 다음 부스팅 단계에서 초깃값 0.1보다 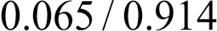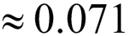로 감소됩니다. 비슷하게 잘못 분류된 샘플의 가중치는 0.1에서 로 증가합니다.