Note ≡ 선형대수 기초: 점곱과 행렬 전치

이어지는 절에서는 기초적인 선형대수 표기법을 자주 사용합니다. 예를 들어 x와 w 값을 곱해 더한 것을 벡터 점곱(dot product)으로 간략히 나타냅니다. 위 첨자 T는 열 벡터를 행 벡터로 또는 그 반대로 바꾸는 전치(transpose)를 의미합니다. 예를 들어 다음과 같은 두 열 벡터가 있다고 가정해 보죠.

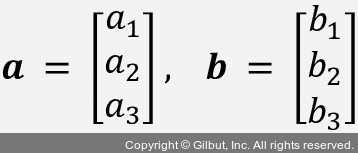
그러면 벡터 a의 전치를 a^T = [a₁ a₂ a₃]으로 쓰고 점곱을 다음과 같이 쓸 수 있습니다.

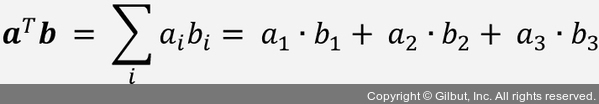
또한, 전치 연산은 행렬에 적용하여 대각 원소를 기준으로 반전시킬 수 있습니다. 예를 들어 다음과 같습니다.

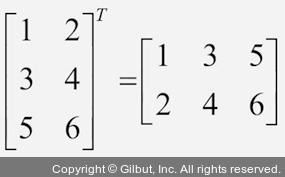
전치 연산은 행렬에서만 정의되어 있습니다. 하지만 머신 러닝 분야에서는 n×1 또는 1×m 행렬을 ‘벡터’라고 합니다. 책에서는 아주 기초적인 선형대수만 사용합니다. 빠르게 기억을 되살리려면 지코 콜터(Zico Kolter)가 쓴 훌륭한 선형대수 소개 자료인 “Linear Algebra Review and Reference”(http://www.cs.cmu.edu/~zkolter/course/linalg/linalg_notes.pdf)를 참고하세요.