퍼셉트론은 두 클래스가 선형적으로 구분될 때, 즉 두 클래스가 선형 결정 경계로 완벽하게 나뉠 수 있는 경우에만 수렴이 보장됩니다. (관심 있는 독자는 제 강의 노트에서 수학 증명을 볼 수 있습니다. https://sebastianraschka.com/pdf/lecture-notes/stat479ss19/L03_perceptron_slides.pdf) 그림 2-3은 선형적으로 구분되는 데이터와 그렇지 못한 데이터의 예를 보여 줍니다.

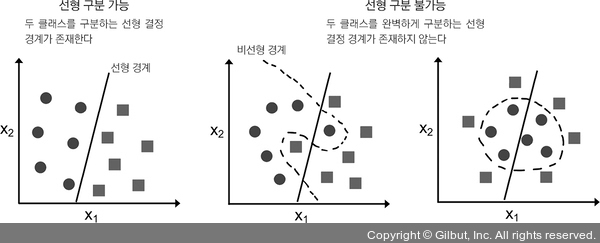
▲ 그림 2-3 선형적으로 구분되는 데이터셋과 그렇지 못한 클래스의 예

두 클래스를 선형 결정 경계로 나눌 수 없다면 훈련 데이터셋을 반복할 최대 횟수(에포크(epoch))를 지정하고 분류 허용 오차를 지정할 수 있습니다. 그렇지 않으면 퍼셉트론은 가중치 업데이트를 멈추지 않습니다. 나중에 이 장에서 클래스가 선형적으로 완벽하게 구분되지 않더라도 선형 결정 경계를 만들고 수렴하는 아달린(Adaline) 알고리즘을 다루겠습니다. 3장에서는 비선형 결정 경계를 만들 수 있는 알고리즘에 대해 배우겠습니다.