다음 장에서는 항등 함수가 아니고 비선형 활성화 함수를 사용하는 로지스틱 회귀 분류기를 배울 것입니다. 로지스틱 회귀 모델은 활성화 함수와 손실 함수만 다르고 아달린과 매우 비슷합니다.
이전 퍼셉트론 구현과 마찬가지로 손실 값을 self.losses_ 리스트에 모아서 훈련이 끝난 후 알고리즘이 수렴하는지 확인해 보겠습니다.
Note ≡ 행렬 곱셈
행렬-벡터 곱셈은 벡터 점곱을 계산하는 것과 비슷합니다. 행렬의 각 행을 하나의 행 벡터처럼 취급합니다. 이런 벡터화된 방식은 간결한 기호로 표현할 수 있고 넘파이를 사용하여 매우 효율적으로 계산할 수 있습니다. 예를 들어 다음과 같습니다.
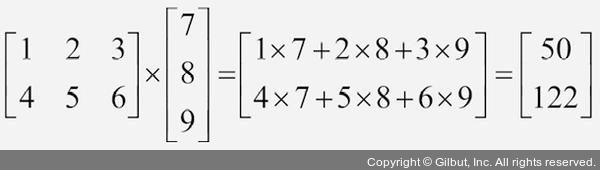
이 식에서 행렬과 벡터를 곱했지만 수학적으로는 정의되지 않습니다. 그러나 관례상 이런 벡터를 3×1 행렬로 간주합니다.
실전에서는 최적으로 수렴하는 좋은 학습률 η를 찾기 위해 여러 번 실험을 해야 합니다. 두 개의 학습률 η = 0.1과 η = 0.0001을 선택해 보죠. 에포크 횟수 대비 손실 함수의 값을 그래프로 나타내면 아달린 구현이 훈련 데이터에서 얼마나 잘 학습하는지 볼 수 있습니다.