앞의 식은 로그 오즈와 최종 입력 사이에 선형 관계에 대한 가정을 나타내지만 실제 관심 대상은 샘플의 클래스 소속 확률인 p입니다. logit 함수는 확률을 실수에 매핑하므로 이 함수의 역함수를 사용하여 실수 범위를 확률 p에 대한 [0, 1] 범위로 다시 매핑할 수 있습니다.
logit 함수를 거꾸로 뒤집은 함수를 로지스틱 시그모이드 함수(logistic sigmoid function)라고 합니다. 함수 모양이 S자 형태를 띠기 때문에 간단하게 줄여서 시그모이드 함수(sigmoid function)라고도 합니다.
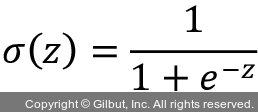
여기에서 z는 가중치와 입력(즉, 훈련 샘플의 특성)의 선형 조합으로 이루어진 최종 입력입니다.
z = wTx + b입니다.
시그모이드 함수가 어떤 모습인지 -7에서 7까지 그려 보겠습니다.