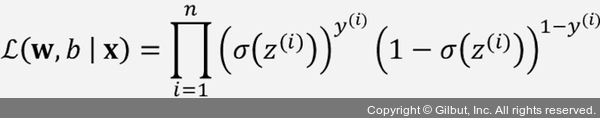Note ≡ 로그 가능도 함수 유도하기

데이터가 주어졌을 때 모델의 가능도 에 대한 표현을 다음과 같이 구할 수 있습니다. 클래스 레이블이 0과 1인 이진 분류 문제일 경우 레이블 1을 베르누이 변수(Bernoulli variable) Y~Bern(p)로 생각할 수 있습니다. 이 변수는 p의 확률로 1 또는 0 두 값을 가질 수 있습니다. 하나의 데이터 포인트에 대해 이 확률을 와 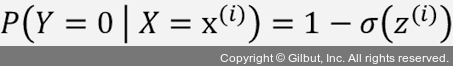로 쓸 수 있습니다.

두 식을 합치고 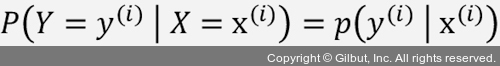를 사용해서 간단히 나타내면 베르누이 변수의 확률 질량 함수를 얻을 수 있습니다.

모든 훈련 샘플이 독립적이라는 가정하에 모든 이벤트가 발생할 확률을 계산하는 곱셈 규칙을 사용하여 훈련 레이블의 가능도를 다음과 같이 쓸 수 있습니다.

이제 베르누이 변수의 확률 질량 함수로 대체하면 모델 파라미터 업데이트를 통해 최대화시킬 가능도 공식을 얻을 수 있습니다.