4.5.2 L 2 규제의 기하학적 해석

이전 절에서 언급한 대로 L2 규제는 손실 함수에 페널티 항(penalty term)을 추가합니다. 규제가 없는 손실 함수로 훈련한 모델에 비해 가중치 값을 아주 작게 만드는 효과를 냅니다.

L1 규제가 어떻게 희소성을 만드는지 잘 이해하기 위해 한 걸음 물러서서 규제의 기하학적 해석에 대해 고찰해 보겠습니다. 두 개의 가중치 값 w₁과 w₂에 대한 볼록한 손실 함수의 등고선을 그려 보죠.

2장 아달린에서 사용했던 제곱 오차합(SSE) 손실 함수를 생각해 보겠습니다. 이 함수는 정답 레이블 y와 예측 클래스 레이블 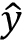사이의 거리를 제곱하고 훈련 세트에 있는 전체 샘플 개수 N으로 나누어 평균을 계산합니다. MSE가 함수가 구 모양이어서 로지스틱 회귀의 손실 함수보다 그리기 쉽습니다. 여기에서 얻은 개념은 로지스틱 회귀에도 동일하게 적용 가능합니다. 그림 4-5와 같이 우리의 목표는 훈련 데이터에서 손실 함수를 최소화하는 가중치 값의 조합을 찾는 것임을 기억하세요(타원의 중심 포인트).¹⁵

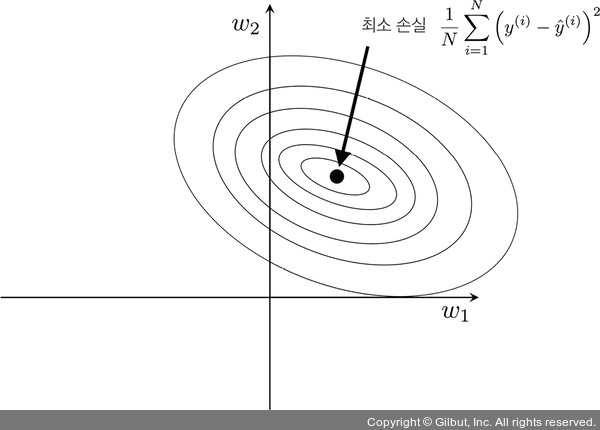
▲ 그림 4-5 평균 제곱 오차 손실 함수 최소화