그림 5-1에서 x₁과 x₂는 원본 특성 축이고 PC1과 PC2는 주성분입니다.

PCA를 사용하여 차원을 축소하기 위해 d×k 차원의 변환 행렬 W를 만듭니다. 이 행렬로 훈련 샘플의 특성 벡터 x를 새로운 k 차원의 특성 부분 공간으로 매핑합니다. 이 부분 공간은 원본 d 차원의 특성 공간보다 작은 차원을 가집니다. 예를 들어 다음과 같은 과정을 따릅니다. 특성 벡터 x가 있다고 가정해 보죠.

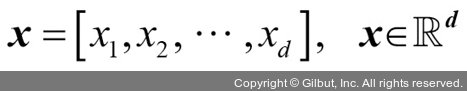
이 벡터는 변환 행렬 에 의해 변환됩니다.

xW = z

출력된 결과 벡터는 다음과 같습니다.

원본 d 차원 데이터를 새로운 k 차원의 부분 공간(일반적으로 k << d)으로 변환하여 만들어진 첫 번째 주성분이 가장 큰 분산을 가질 것입니다. 모든 주성분은 다른 주성분들과 상관관계가 없다는(직교한다는) 제약하에 가장 큰 분산을 가집니다. 입력 특성에 상관관계가 있더라도 만들어진 주성분은 서로 직각을 이룰(상관관계가 없을) 것입니다. PCA 방향은 데이터 스케일에 매우 민감합니다. 특성의 스케일이 다르고 모든 특성의 중요도를 동일하게 취급하려면 PCA를 적용하기 전에 특성을 표준화 전처리해야 합니다.