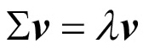여기에서 μ_k와 μ_k는 특성 j와 k의 샘플 평균입니다. 데이터셋을 표준화 전처리했기 때문에 샘플 평균은 0입니다. 두 특성 간 양의 공분산은 특성이 함께 증가하거나 감소하는 것을 나타냅니다. 반면 음의 공분산은 특성이 반대 방향으로 달라진다는 것을 나타냅니다. 예를 들어 세 개의 특성으로 이루어진 공분산 행렬은 다음과 같이 쓸 수 있습니다. (∑는 그리스 문자 시그마의 대문자입니다. 합 기호와 혼동하지 마세요.)

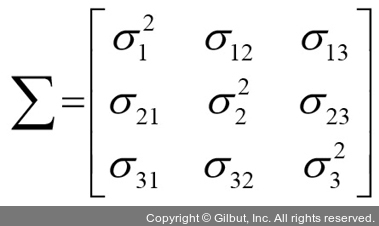
공분산 행렬의 고유 벡터가 주성분(최대 분산의 방향)을 표현합니다.¹ 이에 대응되는 고윳값은 주성분의 크기입니다. Wine 데이터셋의 경우 13×13 차원의 공분산 행렬로부터 13개의 고유 벡터와 고윳값을 얻을 수 있습니다.

이제 세 번째 단계를 위해 공분산 행렬의 고유 벡터와 고윳값의 쌍을 구해 보죠. 선형대수학 수업을 들었다면 고유 벡터 v는 다음 식을 만족한다고 배웠을 것입니다.²