Note ≡ 거울 투영(mirrored projection)

사용하는 넘파이와 LAPACK 버전에 따라 부호가 반대인 행렬 W를 얻을 수 있습니다. 이는 문제가 아닙니다. 만약 v가 행렬 ∑의 고유 벡터이면 다음과 같습니다.

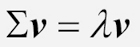
여기에서 v는 고유 벡터고 -v 또한 고유 벡터입니다. 다음과 같이 기초대수학을 사용하면 방정식의 양쪽에 α를 곱할 수 있습니다.

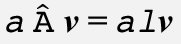
행렬 곱셈은 스칼라 곱셈에 대해 결합법칙이 성립하므로 다음과 같이 다시 정렬할 수 있습니다.

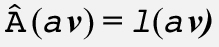
이렇게 쓰면 αv는 α 1과 α = -1일 때 같은 고윳값 λ를 갖는 고유 벡터임을 알 수 있습니다.