이 코드를 실행하면 두 개의 주성분 축으로 줄어든 훈련 데이터에서 만든 결정 경계를 볼 수 있습니다.

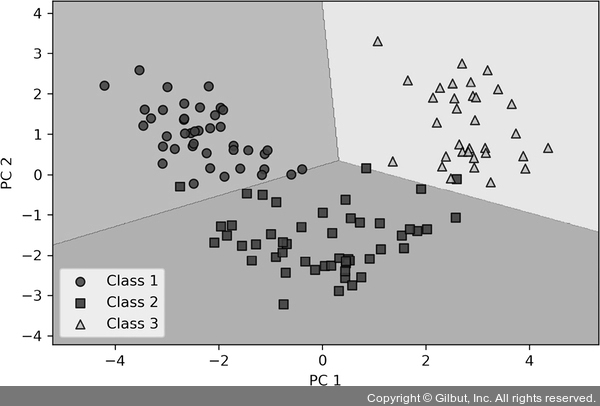
▲ 그림 5-4 차원 축소를 위해 사이킷런의 PCA를 적용한 후 훈련 샘플과 로지스틱 회귀의 결정 경계

사이킷런의 PCA 투영과 우리가 직접 만든 PCA 구현을 비교했을 때 두 그래프가 거울에 비친 것처럼 뒤집힌 경우가 있습니다. 두 그래프 중 하나에 문제가 있기 때문이 아니고 계산 방법에 따라 고유 벡터는 음수나 양수 부호를 가질 수 있기 때문입니다.

이것이 문제가 되지 않지만 필요하다면 데이터에 -1을 곱해서 이미지를 뒤집을 수 있습니다. 고유 벡터는 일반적으로 단위 길이가 1이 되도록 정규화되어 있습니다. 예제를 마무리하기 위해 테스트 데이터셋을 변환하고 로지스틱 회귀가 클래스를 잘 구분하는지 결정 경계를 그려 봅시다.