그림 2-5와 같이 입력과 출력을 배치해 보면 어떤 크기의 점곱이 가능한지 이해하는 데 도움이 됩니다.

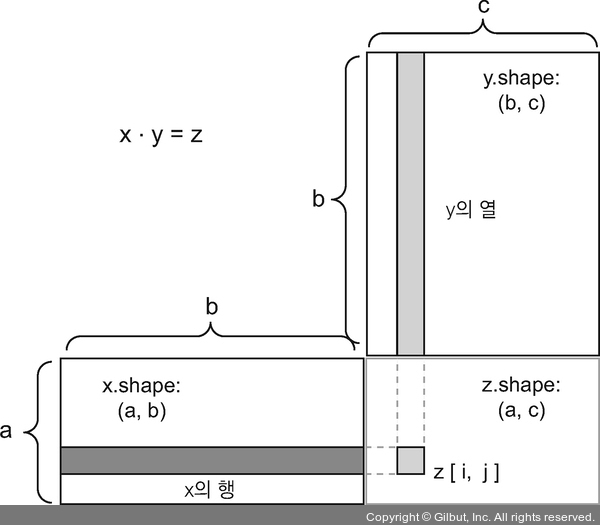
▲ 그림 2-5 행렬 점곱 다이어그램

이 그림에서 x, y, z는 직사각형 모양으로 그려져 있습니다(원소들이 채워진 박스라고 생각하면 됩니다). x의 행 벡터와 y의 열 벡터가 같은 크기여야 하므로 자동으로 x의 너비는 y의 높이와 동일해야 합니다. 새로운 머신 러닝 알고리즘을 개발할 때 이런 그림을 자주 그리게 될 것입니다.

더 일반적으로는 앞서 설명한 2D의 경우처럼 크기를 맞추는 동일한 규칙을 따르면 다음과 같이 고차원 텐서 간의 점곱을 할 수 있습니다.

(a, b, c, d) . (d,) -> (a, b, c)
(a, b, c, d) . (d, e) -> (a, b, c, e)