또한, 이 함수가 매끈하므로(곡선의 각도가 갑자기 바뀌지 않습니다) epsilon_x가 충분히 작다면 어떤 포인트 p에서 기울기 a의 선형 함수로 f를 근사할 수 있습니다. 따라서 epsilon_y는 a * epsilon_x가 됩니다.

f(x + epsilon_x) = y + a * epsilon_x

이 선형적인 근사는 x가 p에 충분히 가까울 때 유효합니다.

이 기울기를 p에서 f의 도함수(derivative)라고 합니다. 이는 a가 음수일 때 p에서 양수 x만큼 조금 이동하면 f(x)가 감소한다는 것을 의미합니다(그림 2-17). a가 양수일 때는 음수 x만큼 조금 이동하면 f(x)가 감소됩니다. a의 절댓값(도함수의 크기)은 이런 증가나 감소가 얼마나 빠르게 일어날지 알려 줍니다.

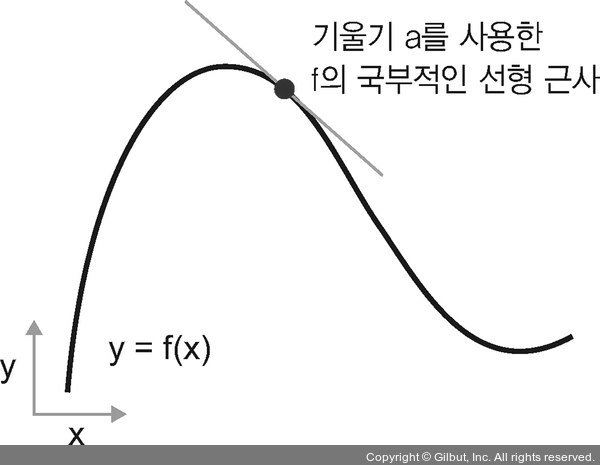
▲ 그림 2-17 p에서 f의 도함수