계산 그래프를 활용한 자동 미분

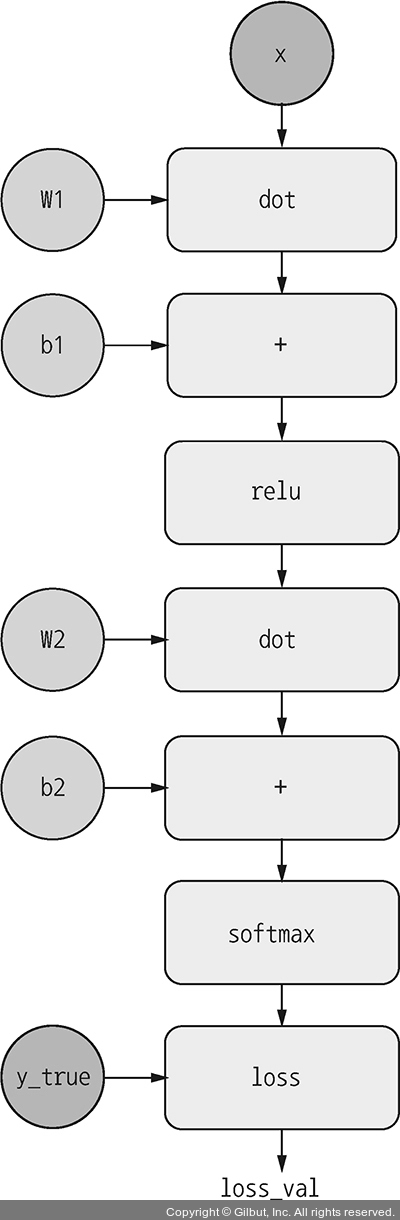
▲ 그림 2-21 2개의 층으로 구성된 모델의 계산 그래프 표현

역전파를 계산 그래프(computation graph) 관점에서 생각하면 좋습니다. 계산 그래프는 텐서플로와 일반적인 딥러닝 혁신의 중심에 있는 데이터 구조입니다. 이는 연산(여기에서는 텐서 연산)의 유향 비순환 그래프(directed acyclic graph)입니다.²⁷ 예를 들어 그림 2-21은 이 장에서 첫 번째로 만든 모델의 그래프 표현입니다.

계산 그래프를 사용하면 계산을 데이터로 다룰 수 있기 때문에 컴퓨터 과학 분야에서 매우 성공적인 추상화 방법입니다. 계산 가능한 표현은 기계가 인식할 수 있는 데이터 구조로 인코딩되어 다른 프로그램의 입력이나 출력으로 사용할 수 있습니다. 예를 들어 계산 그래프를 입력으로 받고 동일한 계산을 대규모 분산 버전으로 구현한 새로운 계산 그래프를 반환하는 프로그램을 생각해 볼 수 있습니다(이는 직접 분산 로직을 작성하지 않고 어떤 계산도 분산시킬 수 있다는 의미입니다). 또는 계산 그래프를 받고 이 그래프가 표현하는 식의 도함수를 자동으로 생성하는 프로그램을 상상해 보세요. 계산을 .py 파일의 한 줄에 ASCII 문자로 작성하는 것이 아니라 명시적인 그래프 데이터 구조로 표현한다면 이런 작업이 훨씬 쉬워집니다.

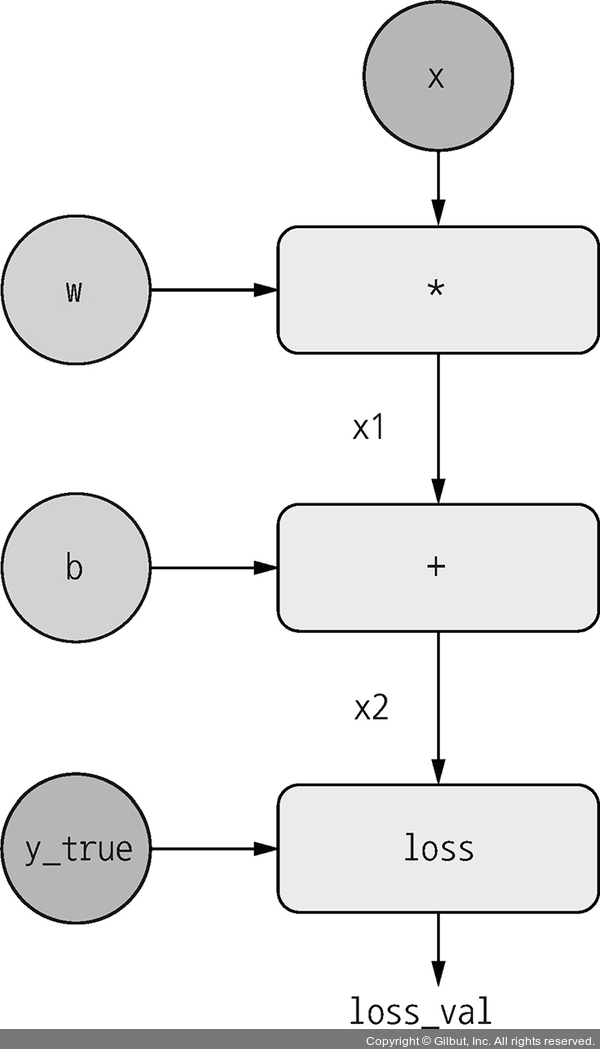
▲ 그림 2-22 간단한 계산 그래프 예