구현을 간단하게 하기 위해 미니 배치 훈련 대신 배치 훈련을 사용하겠습니다. 즉, 데이터를 작은 배치로 나누어 반복하지 않고 전체 데이터를 사용하여 훈련 스텝(그레이디언트 계산과 가중치 업데이트)을 실행합니다. 이렇게 하면 한 번에 2,000개의 샘플에 대해 정방향 패스와 그레이디언트를 계산해야 하므로 각 훈련 스텝의 실행 시간이 오래 걸립니다. 한편으로는 가령 128개의 랜덤한 샘플을 사용하지 않고 전체 훈련 샘플로부터 정보를 취합하므로 각각의 그레이디언트 업데이트는 훈련 데이터의 손실을 감소하는 데 훨씬 더 효과적입니다. 결과적으로 훈련 스텝의 횟수가 많이 필요하지 않고 미니 배치 훈련 때보다 일반적으로 큰 학습률을 사용할 수 있습니다(코드 3-20에서 정의한 learning_rate = 0.1을 사용하겠습니다).

코드 3-21 배치 훈련 루프

for step in range(40):
    loss = training_step(inputs, targets)
    print(f"{step}번째 스텝의 손실: {loss:.4f}")

40번 에포크 후 훈련 손실이 0.025에서 안정화되는 것 같습니다. 이 선형 모델이 훈련 데이터 포인트를 어떻게 분류하는지 그려 보죠. 타깃이 0 또는 1이기 때문에 입력 포인트의 예측 값이 0.5보다 작으면 ‘0’으로 분류되고 0.5보다 크면 ‘1’로 분류됩니다(그림 3-7).

predictions = model(inputs)
plt.scatter(inputs[:, 0], inputs[:, 1], c=predictions[:, 0] > 0.5)
plt.show()

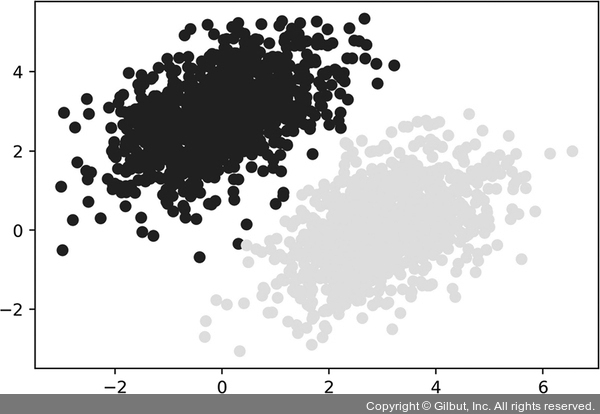
▲ 그림 3-7 훈련 입력에 대한 모델의 예측: 훈련 타깃과 매우 비슷하다