y = ax2의 그래프를 x축 방향으로 p만큼, y축 방향으로 q만큼 평행 이동시키면 그림 3-3과 같이 움직입니다. 점 p와 q를 꼭짓점으로 하는 포물선이 되겠지요. 이때 포물선의 맨 아래에 위치한 지점이 최솟값이 되는데, 딥러닝을 실행할 때는 이 최솟값을 찾아내는 과정이 매우 중요합니다.
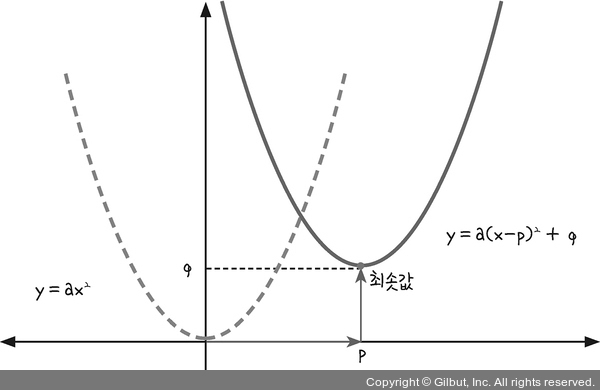
그림 3-3 | 이차 함수 그래프의 평행 이동과 최솟값
이 최솟값은 4장에 소개할 ‘최소 제곱법’ 공식으로 쉽게 알아낼 수 있습니다. 그런데 딥러닝을 실제로 실행할 때 만나는 문제에서는 대부분 최소 제곱법을 활용할 수가 없습니다. 그 이유는 최소 제곱법을 계산하기 위해 꼭 필요한 조건들을 알 수 없기 때문입니다. 따라서 미분과 기울기를 이용해야 합니다.

















