3 미분, 순간 변화율과 기울기

딥러닝을 이해하는 데 가장 중요한 수학 원리는 미분이라고 할 수 있습니다. 조금 전 딥러닝은 결국 일차 함수의 a와 b 값을 구하는 것인데, a와 b 값은 이차 함수 포물선의 최솟값을 구하는 것이라고 했지요. (지금은 이해가 안 되어도 괜찮습니다. 5장에서 자세히 설명합니다.) 이 최솟값을 미분으로 구하기 때문에 미분이 딥러닝에서 중요한 것입니다. 미분과 기울기의 개념을 먼저 알아보겠습니다.

그림 3-4와 같이 y = x²이라는 그래프가 있다고 해 봅시다. x축에 있는 한 점 a에 대응하는 y의 값은 a²이겠지요. 이때 a가 오른쪽이나 왼쪽으로 조금씩 이동한다고 상상해 봅시다. 그러면 이에 따라 y도 조금씩 변화할 것입니다.

상상력을 조금 더 발휘해 이번에는 a가 미세하게 ‘0에 가까울 만큼’ 움직였다고 합시다. 그러면 y 값 역시 매우 미세하게 변화를 할 텐데, 이번에는 너무 미세해서 실제로 움직이는 것이 아니라 방향만 드러내는 정도의 순간적인 변화만 있을 것입니다. 이 순간의 변화를 놓고 순간 변화율이라는 이름을 붙였습니다. 순간 변화율은 어느 쪽을 향하는 방향성을 지니고 있으므로, 이 방향을 따라 직선을 길게 그려 주면 그래프와 맞닿는 접선이 그려집니다. 이 선이 바로 이 점에서의 기울기가 됩니다.

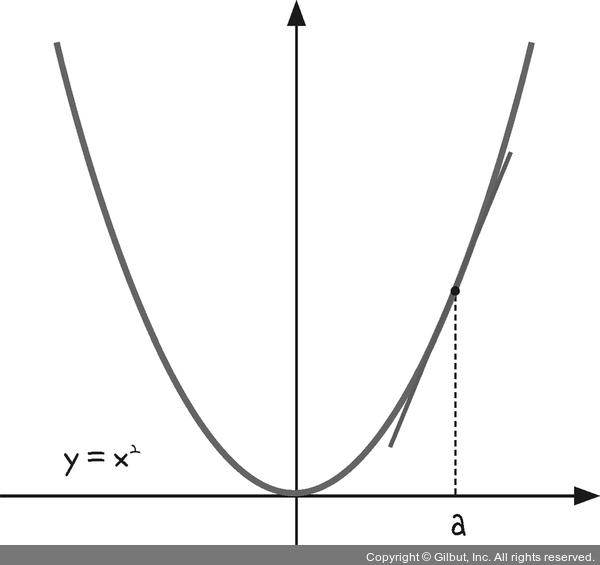
그림 3-4 | a에서의 순간 변화율은 곧 기울기다!