미분을 한다는 것은 쉽게 말해 이 ‘순간 변화율’을 구한다는 것입니다. 어느 순간에 어떤 변화가 일어나고 있는지 숫자로 나타낸 것을 미분 계수라고 하며, 이 미분 계수는 곧 그래프에서의 기울기를 의미합니다. 이 기울기가 중요한 것은 기울기가 0일 때, 즉 x축과 평행한 직선으로 그어질 때가 바로 그래프에서 최솟값인 지점이 되기 때문입니다.

이제 순간 변화율을 구하는 방법을 알아보겠습니다. 어떤 함수 f(x)가 그림 3-5와 같이 주어졌다고 합시다. 이 함수에 x축 위의 두 실수 a와 b를 대입하면 두 점 A, B는 그림과 같이 각각 A(a, f(a)), B(b, f(b))에 해당하는 곳에 표시됩니다.

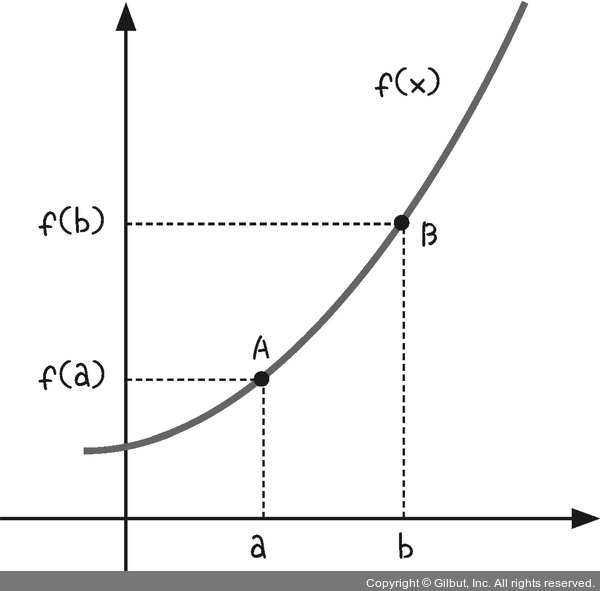
그림 3-5 | 함수 f(x)의 x축 위에 두 실수 a와 b를 대입