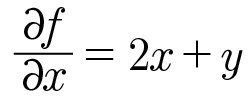4 편미분

미분과 더불어 딥러닝을 공부할 때 가장 자주 접하게 되는 또 다른 수학 개념은 바로 편미분입니다. 미분과 편미분 모두 ‘미분하라’는 의미에서는 다를 바가 없습니다. 그러나 여러 가지 변수가 식 안에 있을 때, 모든 변수를 미분하는 것이 아니라 우리가 원하는 한 가지 변수만 미분하고 그 외에는 모두 상수로 취급하는 것이 바로 편미분입니다. 예를 들어 f(x) = x와 같은 식을 미분할 때는 변수가 x 하나뿐이어서 미분하라는 의미에 혼란이 없습니다. 그러나 다음 식을 보겠습니다.

f(x, y) = x² + yx + a (a는 상수)

여기에는 변수가 x와 y, 이렇게 두 개 있습니다. 그러면 이 중 어떤 변수로 미분해야 하는지 정해야 하므로 편미분을 사용하는 것입니다. 만일 이 식처럼 여러 변수 중에서 x에 관해서만 미분하고 싶다면, 함수 f 를 ‘x에 관해 편미분하라’고 하며 다음과 같이 식을 씁니다.

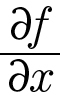
그러면 앞에 나온 함수 f(x, y) = x² + yx + a를 x에 관해 편미분하는 과정은 어떻게 될까요? 먼저 바로 앞에서 배운 미분의 성질 4에 따라 x²항은 2x가 됩니다. 그리고 미분법의 기본 공식 3에 따라 yx는 y가 됩니다. 마지막 항 a는 미분의 성질 1에 따라 0이 됩니다. 이를 정리하면 다음과 같이 나타낼 수 있습니다.

f(x, y) = x² + yx + a일 때