6 시그모이드 함수

딥러닝의 내부를 보면 입력받은 신호를 얼마나 출력할지를 계산하는 과정이 무수히 반복됩니다. 이때 출력 값으로 얼마나 내보낼지를 계산하는 함수를 활성화 함수라고 합니다. 활성화 함수는 딥러닝이 발전함에 따라 여러 가지 형태로 개발되어 왔는데, 그중 가장 먼저 배우는 중요한 함수가 바로 시그모이드 함수입니다. 시그모이드 함수는 지수 함수에서 밑 값이 자연 상수 e인 함수를 의미합니다. 자연 상수 e는 ‘자연 로그의 밑’, ‘오일러의 수’ 등 여러 이름으로 불리는데, 파이(π)처럼 수학에서 중요하게 사용되는 무리수이며 그 값은 대략 2.718281828…입니다.

자연 상수 e가 지수 함수에 포함되어 분모에 들어가면 시그모이드 함수가 되는데, 이를 식으로 나타내면 다음과 같습니다.

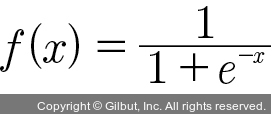
시그모이드 함수를 그래프로 그려 보면 그림 3-8과 같이 S자 형태로 나타납니다.

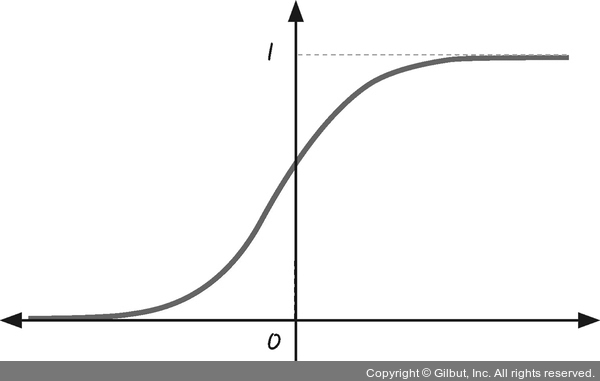
그림 3-8 | 시그모이드 함수의 그래프

x가 큰 값을 가지면 f(x)는 1에 가까워지고, x가 작은 값을 가지면 f(x)는 0에 가까워집니다. S자 형태로 그려지는 이 함수의 속성은 0 또는 1, 두 개의 값 중 하나를 고를 때 유용하게 쓰입니다. 6장의 ‘참 거짓 판단 장치’ 편에서 중요하게 다룰 함수입니다.