5 평균 제곱 오차

최소 제곱법을 이용해 기울기 a와 y 절편을 편리하게 구했지만, 이 공식만으로 앞으로 만나게 될 모든 상황을 해결하기는 어렵습니다. 여러 개의 입력을 처리하기에는 무리가 있기 때문입니다. 예를 들어 앞서 살펴본 예에서는 변수가 ‘공부한 시간’ 하나뿐이지만, 2장에서 살펴본 폐암 수술 환자의 생존율 데이터를 보면 입력 데이터의 종류가 17개나 됩니다. 딥러닝은 대부분 입력 값이 여러 개인 상황에서 이를 해결하기 위해 실행되기 때문에 기울기 a와 y 절편 b를 찾아내는 다른 방법이 필요합니다.

가장 많이 사용하는 방법은 ‘일단 그리고 조금씩 수정해 나가기’ 방식입니다. 가설을 하나 세운 후 이 값이 주어진 요건을 충족하는지 판단해서 조금씩 변화를 주고, 이 변화가 긍정적이면 오차가 최소가 될 때까지 이 과정을 계속 반복하는 방법입니다. 이는 딥러닝을 가능하게 하는 가장 중요한 원리 중 하나입니다.

그런데 선을 긋고 나서 수정하는 과정에서 빠지면 안 되는 것이 있습니다. 나중에 그린 선이 먼저 그린 선보다 더 좋은지 나쁜지를 판단하는 방법입니다. 즉, 각 선의 오차를 계산할 수 있어야 하고, 오차가 작은 쪽으로 바꾸는 알고리즘이 필요한 것이지요.

이를 위해 주어진 선의 오차를 평가하는 방법이 필요합니다. 오차를 구할 때 가장 많이 사용되는 방법이 평균 제곱 오차(Mean Square Error, MSE)입니다. 지금부터 평균 제곱 오차를 구하는 방법을 알아보겠습니다. 앞서 나온 공부한 시간과 성적의 관계도를 다시 한 번 볼까요?

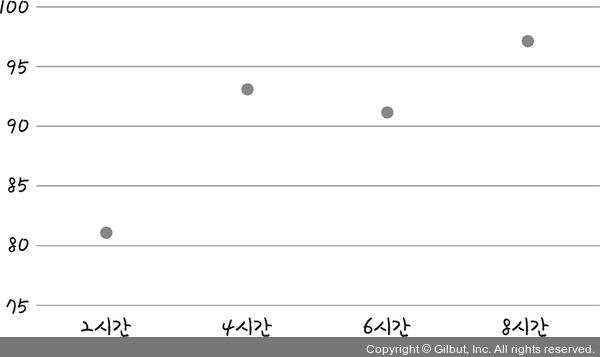
그림 4-5 | 공부한 시간과 성적의 관계도