이렇게 해서 구한 오차를 모두 더하면 1 + (-5) + 3 + 3 = 2가 됩니다. 그런데 이 값은 오차가 실제로 얼마나 큰지를 가늠하기에는 적합하지 않습니다. 오차에 양수와 음수가 섞여 있어 오차를 단순히 더해 버리면 합이 0이 될 수도 있기 때문입니다. 부호를 없애야 정확한 오차를 구할 수 있습니다. 따라서 오차의 합을 구할 때는 각 오차 값을 제곱해 줍니다. 이를 식으로 표현하면 다음과 같습니다.

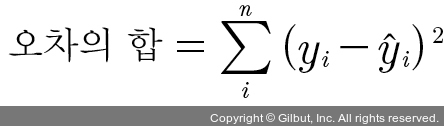
여기서 i는 x가 나오는 순서를, n은 x 원소의 총 개수를 의미합니다. y_i는 x_i에 대응하는 ‘실제 값’이고 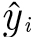는 x_i가 대입되었을 때 직선의 방정식(여기서는 y = 3x + 76)이 만드는 ‘예측 값’입니다. 이 식으로 오차의 합을 다시 계산하면 1 + 25 + 9 + 9 = 44입니다.

우리가 구하고자 하는 평균 제곱 오차는 위에서 구한 오차의 합을 n으로 나눈 것입니다.

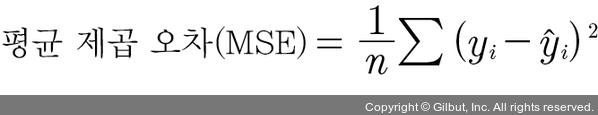
이 식은 앞으로 머신 러닝과 딥러닝을 공부할 때 자주 등장할 중요한 식입니다. 앞서 구한 오차의 합(=44)과 x 원소의 총 개수(=4)를 이 식에 대입하면 ¼ × 44 = 11이란 값이 나옵니다. 이로써 우리가 그은 임의의 직선이 11이라는 평균 제곱 오차를 갖는 직선이었다는 것을 알 수 있습니다.

이제 우리의 작업은 11보다 작은 평균 제곱 오차를 가지게 만드는 a 값과 b 값을 찾는 것이 되었습니다. 이렇듯 선형 회귀란 임의의 직선을 그어 이에 대한 평균 제곱 오차를 구하고, 이 값을 가장 작게 만들어 주는 a 값과 b 값을 찾아가는 작업입니다.