1 경사 하강법의 개요

‘3장. 딥러닝을 위한 기초 수학’에서 미분은 한 점에서의 순간 기울기라고 배웠습니다.

y = x² 그래프에서 x에 다음과 같이 a₁, a₂ 그리고 m을 대입해 그 자리에서 미분하면 그림 5-2와 같이 각 점에서의 순간 기울기가 그려집니다.

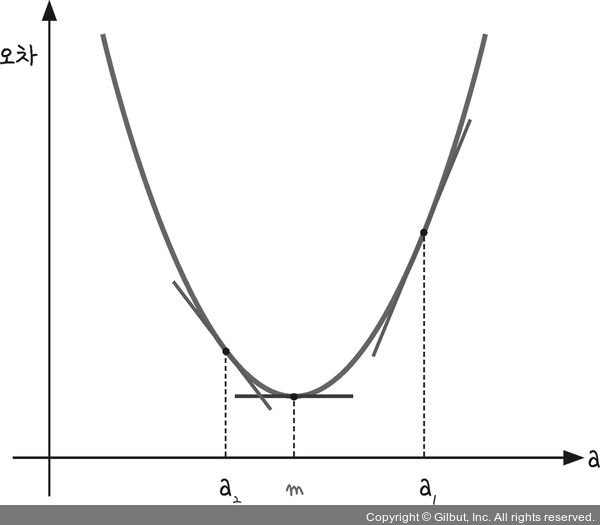
그림 5-2 | 순간 기울기가 0인 점이 곧 우리가 찾는 최솟값 m이다

여기서 눈여겨보아야 할 것은 우리가 찾는 최솟값 m에서의 순간 기울기입니다. 그래프가 이차 함수 포물선이므로 꼭짓점의 기울기는 x축과 평행한 선이 됩니다. 즉, 기울기가 0입니다. 따라서 우리가 할 일은 ‘미분 값이 0인 지점’을 찾는 것이 됩니다.

이를 위해 다음 과정을 거칩니다.

1 | a₁에서 미분을 구한다.

2 | 구한 기울기의 반대 방향(기울기가 +면 음의 방향, -면 양의 방향)으로 얼마간 이동시킨 a₂에서 미분을 구한다(그림 5-3 참조).

3 | 앞에서 구한 미분 값이 0이 아니면 1과 2 과정을 반복한다.