3 다중 선형 회귀의 개요
앞서 학생들이 공부한 시간에 따른 예측 직선을 그리고자 기울기 a와 y 절편 b를 구했습니다. 그런데 이 예측 직선을 이용해도 실제 성적 사이에는 약간의 오차가 있었습니다. 4시간 공부한 친구는 88점을 예측했는데 이보다 좋은 93점을 받았고, 6시간 공부한 친구는 93점을 받을 것으로 예측했지만 91점을 받았습니다. 이러한 차이가 생기는 이유는 공부한 시간 이외의 다른 요소가 성적에 영향을 끼쳤기 때문입니다.
더 정확한 예측을 하려면 추가 정보를 입력해야 하며, 정보를 추가해 새로운 예측 값을 구하려면 변수 개수를 늘려 다중 선형 회귀를 만들어 주어야 합니다.
예를 들어 일주일 동안 받는 과외 수업 횟수를 조사해서 이를 기록해 보았습니다.
표 5-1 | 공부한 시간, 과외 수업 횟수에 따른 성적 데이터
|
공부한 시간(x1) |
2 |
4 |
6 |
8 |
|
과외 수업 횟수(x2) |
0 |
4 |
2 |
3 |
|
성적(y) |
81 |
93 |
91 |
97 |
그럼 지금부터 독립 변수 x1과 x2가 두 개 생긴 것입니다. 이를 사용해 종속 변수 y를 만들 경우 기울기를 두 개 구해야 하므로 다음과 같은 식이 나옵니다.
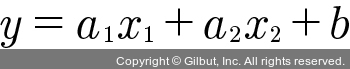
그러면 두 기울기 a1과 a2는 각각 어떻게 구할 수 있을까요? 앞서 배운 경사 하강법을 그대로 적용하면 됩니다. 바로 파이썬 코드로 확인해 보겠습니다.

















