3 오차 공식

이제 우리에게 주어진 과제는 또다시 a 값과 b 값을 구하는 것임을 알았습니다. 시그모이드 함수에서 a 값과 b 값을 어떻게 구해야 할까요? 답은 역시 경사 하강법입니다.

경사 하강법은 먼저 오차를 구한 후 오차가 작은 쪽으로 이동시키는 방법이라고 했습니다. 그렇다면 이번에도 예측 값과 실제 값의 차이, 즉 오차를 구하는 공식이 필요합니다. 그러면 이번에도 앞서 배웠던 평균 제곱 오차를 사용하면 될까요? 안타깝게도 이번에는 평균 제곱 오차를 사용할 수 없습니다. 오차 공식을 도출하기 위해 시그모이드 함수 그래프의 특징을 다시 한 번 살펴보겠습니다.

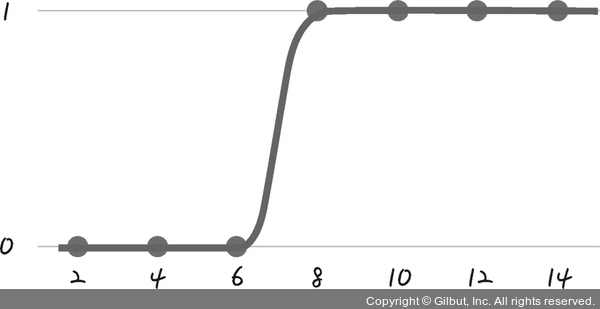
그림 6-7 | 시그모이드 함수 그래프

시그모이드 함수의 특징은 y 값이 0과 1 사이라는 것입니다. 따라서 실제 값이 1일 때 예측 값이 0에 가까워지면 오차가 커집니다. 반대로 실제 값이 0일 때 예측 값이 1에 가까워지는 경우에도 오차는 커집니다. 이를 공식으로 만들 수 있게 하는 함수가 바로 로그 함수입니다.