먼저 출력 부분에 대해 알아보겠습니다. 이전까지 우리는 출력이 0~1 중 하나의 값으로 나왔습니다. 예를 들어 당뇨인지 아닌지에 대한 예측 값이 시그모이드 함수를 거치며 0~1 사이의 값 중 하나로 변환되어 0.5 이상이면 당뇨로, 이하이면 정상으로 판단했지요. 이항 분류의 경우 출력 값이 하나면 되었습니다. 그런데 이번 예제에서는 예측해야 할 값이 세 가지로 늘었습니다. 즉, 각 샘플마다 이것이 setosa일 확률, versicolor일 확률, 그리고 virginica일 확률을 따로따로 구해야 한다는 것이지요. 예를 들어 예측 결과는 그림 12-5와 같은 형태로 나타납니다.

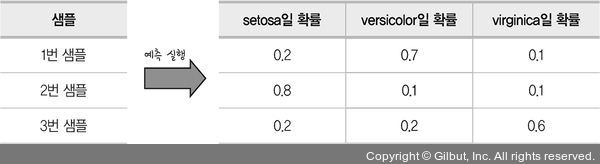
그림 12-5 | 소프트맥스

이렇게 세 가지의 확률을 모두 구해야 하므로 시그모이드 함수가 아닌 다른 함수가 필요합니다. 이때 사용되는 함수가 바로 소프트맥스 함수입니다. 소프트맥스 함수는 그림 12-5와 같이 각 항목당 예측 확률을 0과 1 사이의 값으로 나타내 주는데, 이때 각 샘플당 예측 확률의 총합이 1인 형태로 바꾸어 주게 됩니다(예를 들어 1번 샘플의 경우 0.2 + 0.7 + 0.1 = 1이 됩니다). activation란에 ‘softmax’라고 적어 주는 것으로 소프트맥스 함수를 바로 적용할 수 있습니다.

마찬가지로 손실 함수도 이전과는 달라져야 합니다. 이항 분류에서 binary_crossentropy를 썼다면, 다항 분류에서는 categorical_crossentropy를 쓰면 됩니다.