Note ≡ | 텐서를 메모리에 저장하기

텐서는 그것이 1차원이든 N차원이든 메모리에 저장할 때는 1차원 배열 형태가 됩니다. 즉, 1차원 배열 형태여야만 메모리에 저장할 수 있습니다. 그리고 변환된 1차원 배열을 스토리지(storage)라고 합니다. 스토리지를 이해하기 위해서는 오프셋과 스트라이드 개념을 알아야 합니다.

• 오프셋(offset): 텐서에서 첫 번째 요소가 스토리지에 저장된 인덱스입니다.

• 스트라이드(stride): 각 차원에 따라 다음 요소를 얻기 위해 건너뛰기(skip)가 필요한 스토리지의 요소 개수입니다. 즉, 스트라이드는 메모리에서의 텐서 레이아웃을 표현하는 것으로 이해하면 됩니다. 요소가 연속적으로 저장되기 때문에 행 중심으로 스트라이드는 항상 1입니다.

그렇다면 왜 오프셋과 스트라이드라는 내용을 이해해야 할까요? 선형대수학을 배웠다면 전치 행렬이 무엇인지 알고 있을 것입니다.

간단히 전치 행렬을 설명하면 다음과 같습니다. A 행렬에서 첫 번째 열을 첫 번째 행으로 위치시키고, 두 번째 열을 두 번째 행으로 위치시키며, A^T로 표현합니다(동일한 원리를 텐서에 적용할 수 있습니다).

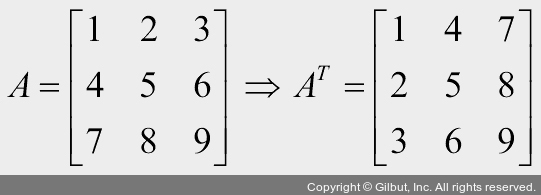
그렇다면 이것이 오프셋, 스트라이드와 무슨 관계가 있을까요?

조금 더 극적인 효과를 위해 행과 열의 수가 다른 텐서 A와 A^T를 생성해 보겠습니다. 그리고 A와 A^T를 1차원 배열로 바꾸어서 메모리에 저장시키기 위해 텐서의 값들을 연속적으로 배치해 보겠습니다.

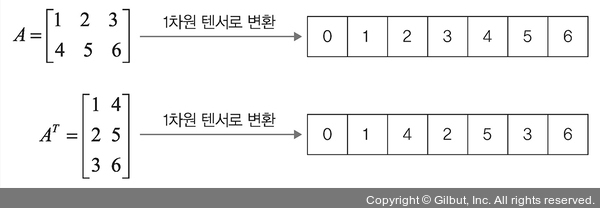
▲ 그림 2-6 3차원 텐서를 1차원으로 변환

A(2×3)와 A^T(3×2)는 다른 형태(shape)를 갖지만 스토리지의 값들은 서로 같습니다. 따라서 A와 A^T를 구분하는 용도로 오프셋과 스트라이드를 사용합니다.

다음 그림의 스토리지에서 2를 얻기 위해서는 1에서 1칸을 뛰어넘어야 하고, 4를 얻기 위해서는 3을 뛰어넘어야 합니다. 따라서 텐서에 대한 스토리지의 스트라이드는 (3, 1)입니다.

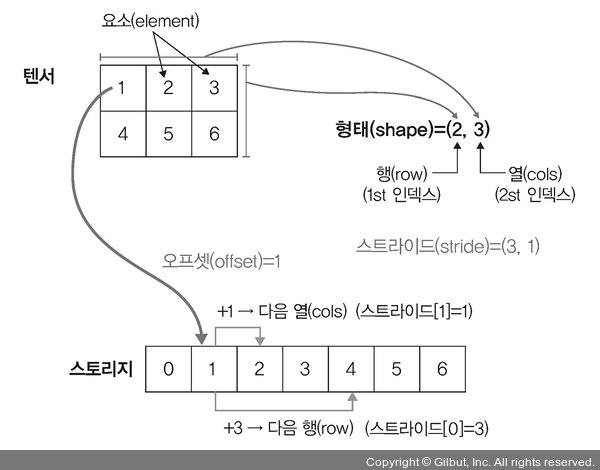
▲ 그림 2-7 A를 1차원으로 변환

반면에 A의 전치 행렬은 좀 다릅니다. 다음 그림의 스토리지에서 4를 얻기 위해서는 1에서 1칸을 뛰어넘어야 하고, 2을 얻기 위해서는 2를 뛰어넘어야 합니다. 따라서 텐서에 대한 스토리지의 스트라이드는 (2, 1)입니다.

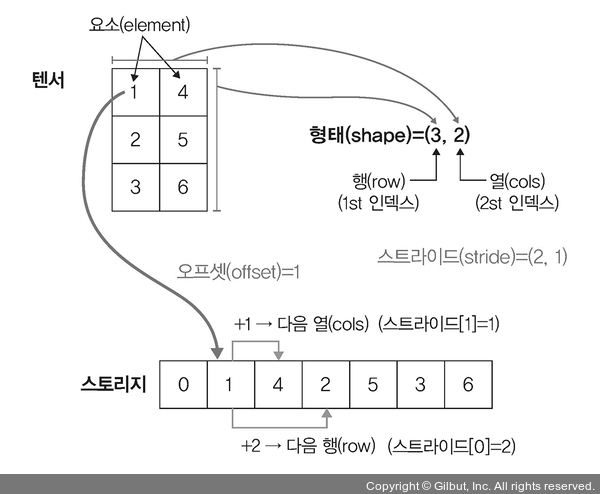
▲ 그림 2-8 A의 전치 행렬을 1차원으로 변환

이와 같이 오프셋과 스트라이드는 데이터 자체가 아닌 행렬/텐서를 구분하기 위해 사용합니다.