Note ≡ | 최소제곱법과 최대우도법

최소제곱법(mean squared)과 최대우도법(maximum likelihood)은 랜덤 표본에서 모집단 모수를 추정하는 데 사용됩니다. 최소제곱법은 일반적인 회귀 분석에서 사용하지만, 최대우도법은 로지스틱 회귀 분석에서 사용합니다. 이 둘 간에 어떤 차이가 있는지 알아봅시다.

최소제곱법은 실제 값에서 예측 값을 뺀 후 제곱해서 구할 수 있습니다(최소제곱법은 1장에서 언급한 평균 제곱 오차와 동일합니다).

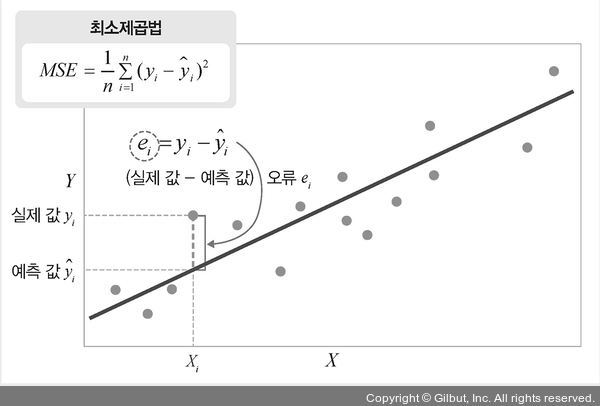
▲ 그림 3-18 최소제곱법

최대우도법을 이해하려면 먼저 우도 개념을 알아야 합니다.

우도(likelihood, 가능도)는 나타난 결과에 따라 여러 가능한 가설을 평가할 수 있는 척도(measure)를 의미합니다. 따라서 최대우도는 나타난 결과에 해당하는 가설마다 계산된 우도 값 중 가장 큰 값입니다. 즉, 일어날 가능성(우도)이 가장 큰 것을 의미합니다. 이 모든 것을 종합하여 최대우도법을 정의하면 최대우도 추정치 또는 최대 가능성 추정량이라고 할 수 있습니다.

최대우도법은 다음 수식으로 구할 수 있습니다.

수식 ①과 같이 입력 값 X와 모델의 파라미터 θ가 주어졌을 때, Y가 나타날 확률을 최대화하는 θ를 찾는 것이 최대우도법입니다. X와 Y가 고정된 상태에서 모델에 X를 넣었을 때 실제 값 Y에 가장 가까운 θ를 찾는 것이 수식입니다. 이때 관측치 m개가 모두 서로 독립이라고 가정할 때, 언더플로⁸를 방지하고자 우도에 로그를 취한다면 최대우도 추정치 수식은 ②와 같습니다.