• 운동량을 조정하는 방법

모멘텀(Momentum)

경사 하강법과 마찬가지로 매번 기울기를 구하지만, 가중치를 수정하기 전에 이전 수정 방향(+, -)을 참고하여 같은 방향으로 일정한 비율만 수정하는 방법입니다. 수정이 양(+)의 방향과 음(-)의 방향으로 순차적으로 일어나는 지그재그 현상이 줄어들고, 이전 이동 값을 고려하여 일정 비율만큼 다음 값을 결정하므로 관성 효과를 얻을 수 있는 장점이 있습니다. 모멘텀은 SGD(확률적 경사 하강법)와 함께 사용합니다.

먼저 확률적 경사 하강법의 수식이 다음과 같다고 합시다.

이때 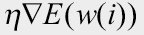수식을 사용하여 가중치를 계산하는데, 기울기 크기와 반대 방향만큼 가중치를 업데이트합니다. 즉, 기울기가 크면 아래쪽(-) 방향으로 업데이트합니다.

또한, SGD 모멘텀(SGD with Momentum)은 확률적 경사 하강법에서 기울기(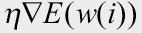)를 속도(v, velocity)로 대체하여 사용하는 방식으로, 이전 속도의 일정 부분을 반영합니다. 즉, 이전에 학습했던 속도와 현재 기울기를 반영해서 가중치를 구합니다.

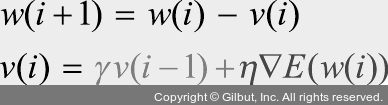
예를 들어 파이토치에서는 다음과 같이 모멘텀을 구현할 수 있습니다.

optimizer = torch.optim.SGD(model.parameters(), lr=0.01, momentum=0.9)

momentum 값은 0.9에서 시작하며 0.95, 0.99처럼 조금씩 증가시키면서 사용합니다.

네스테로프 모멘텀(Nesterov Accelerated Gradient, NAG)

네스테로프 모멘텀은 모멘텀 값과 기울기 값이 더해져 실제 값을 만드는 기존 모멘텀과 달리 모멘텀 값이 적용된 지점에서 기울기 값을 계산합니다. 모멘텀 방법은 멈추어야 할 시점에서도 관성에 의해 훨씬 멀리 갈 수 있는 단점이 있지만, 네스테로프 방법은 모멘텀으로 절반 정도 이동한 후 어떤 방식으로 이동해야 하는지 다시 계산하여 결정하기 때문에 모멘텀 방법의 단점을 극복할 수 있습니다. 따라서 모멘텀 방법의 이점인 빠른 이동 속도는 그대로 가져가면서 멈추어야 할 적절한 시점에서 제동을 거는 데 훨씬 용이합니다.

수식은 다음과 같습니다.

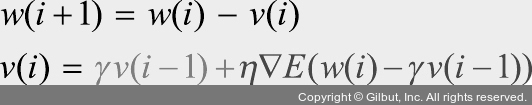
모멘텀과 비슷하지만 속도(v)를 구하는 과정에서 조금 차이가 있습니다. 이전에 학습했던 속도와 현재 기울기에서 이전 속도를 뺀 변화량을 반영해서(더해서) 가중치를 구합니다.

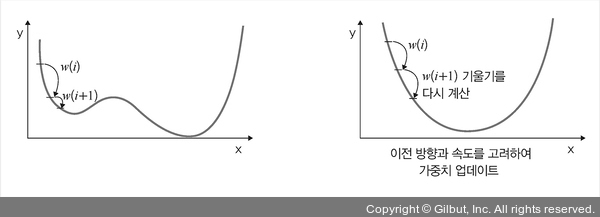
▲ 그림 4-23 모멘텀과 네스테로프 모멘텀

예를 들어 파이토치에서는 다음과 같이 네스테로프 모멘텀을 구현할 수 있습니다.

optimizer = torch.optim.SGD(model.parameters(), lr=0.01, momentum=0.9, nesterov=True) ------ nesterov 기본값은 False