Note ≡ | 계산 그래프
계산 그래프(computational graph)는 이미 2장에서 살펴보았지만 리마인드를 위해 다시 살펴보겠습니다. 계산 그래프란 계산 과정을 그래프로 나타낸 것입니다. 그래프는 여러 개의 노드(node)와 그 노드들을 연결하는 선인 에지(edge)로 구성됩니다.
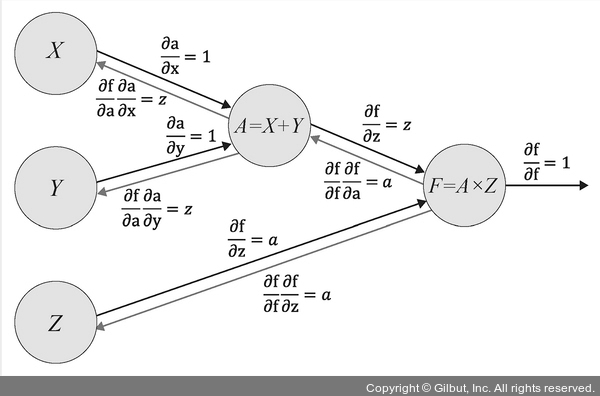
▲ 그림 5-39 계산 그래프
계산 그래프를 사용하는 이유는 두 가지입니다.
• 국소적 계산이 가능합니다. 국소적 계산이 가능하다는 의미는 그림 5-39에서 Z 값이 변경되었다면 X, Y 계산 결과를 그대로 유지한 채로 바뀐 Z의 연산이 필요한 F=A×Z만 계산하면 됩니다.
• 역전파를 통한 미분 계산이 편리합니다. 그림 5-39의 주황색 선이 역전파를 구하는 과정을 보여 주는데 연쇄 법칙(chain rule)을 이용하여 빠르고 간편하게 미분을 계산할 수 있습니다.
Note ≡ | 연쇄 법칙
두 개 이상의 함수가 결합된 함수, 즉 합성 함수의 미분법을 연쇄 법칙 혹은 체인룰(chain rule)이라고 합니다. 예를 들어 다음 그림과 같이 z = (x + y)2을 z = t2과 t = x + y의 합성 함수로 표현하고 각 합성 함수의 미분 결과를 곱한 결과로 나타내는 것이 연쇄 법칙입니다. 합성 함수 및 미분과 관련한 내용은 별도의 인공지능 수학 도서를 참고하세요.
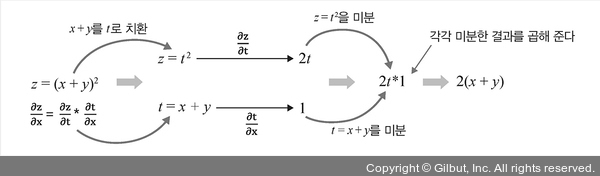
▲ 그림 5-40 합성 함수의 미분