또한, 지금까지 학습한 상태-가치 함수와 행동-가치 함수의 벨만 방정식을 다이어그램으로 표현할 수 있습니다. 이것을 백업 다이어그램이라고 하는데, 다음 그림과 같이 표현합니다.
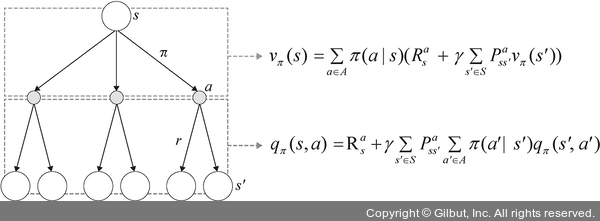
▲ 그림 12-10 백업 다이어그램
상태-가치 함수 vπ(s)는 뒤따를 행동-가치 함수의 정책 기반 가중 평균으로 이해하면 되고, 행동-가치 함수 qπ(s,a)는 다음 상태-가치 함수에 대한 보상과 상태 전이 확률에 대한 결합 확률의 가중 평균으로 이해하면 됩니다.
지금까지 살펴본 벨만 기대 방정식을 좀 더 쉽게 이해할 수 있도록 강화 학습 과정으로 살펴보겠습니다.
1. 처음 에이전트가 접하는 상태 s나 행동 a는 임의의 값으로 설정합니다.
2. 환경과 상호 작용하면서 얻은 보상과 상태에 대한 정보들을 이용하여 어떤 상태에서 어떤 행동을 취하는 것이 좋은지(최대의 보상을 얻을 수 있는지) 판단합니다.
3. 이때 최적의 행동을 판단하는 수단이 상태-가치 함수와 행동-가치 함수이고, 이것을 벨만 기대 방정식을 이용하여 업데이트하면서 점점 높은 보상을 얻을 수 있는 상태와 행동을 학습합니다.
4. 2~3의 과정 속에서 최대 보상을 갖는 행동들을 선택하도록 최적화된 정책을 찾습니다.
따라서 벨만 기대 방정식이 갖는 의미는 미래의 가치 함수 값들을 이용하여 초기화된 임의의 값들을 업데이트하면서 최적의 가치 함수로 다가가는 것입니다. 즉, 강화 학습은 가치 함수 초깃값(0 혹은 랜덤한 숫자들)을 2~3의 과정을 반복하며 얻은 정보들로 업데이트하여 최적의 값을 얻는 것입니다. 그리고 이렇게 반복적으로 얻은 값이 가장 클 때 이를 벨만 최적 방정식이라고 합니다.
이 벨만 최적 방정식을 알아보겠습니다.