오토인코더 개념을 이해했다면 이번에는 수학적으로 접근해 보겠습니다. 미리 이야기하지만 수학적 접근은 언제나 어렵게 느껴질 수 있습니다. 따라서 한 번 읽어 보고 이해하기 어려운 부분들이 있다면 인공지능 수학 관련 도서를 참고하기 바랍니다.

입력 x와 출력 y는 같은 차원(R^d)에 존재한다는 가정하에 입력 데이터를 인코더 네트워크에 통과시켜 압축된 잠재 벡터⁴ z 값을 얻습니다. 이때 z를 구하는 공식은 다음과 같습니다.

z = h(x)

압축된 z 벡터에서 입력 데이터와 크기가 같은 출력 값은 다음과 같이 계산합니다.

y = g(z) = g(h(x))

이때 손실(loss) 값은 입력 값 x와 디코더를 통과한 y 값의 차이로 다음과 같이 계산합니다.

즉, 디코더 네트워크를 통과한 출력 값은 입력 값의 크기와 같아야 합니다.

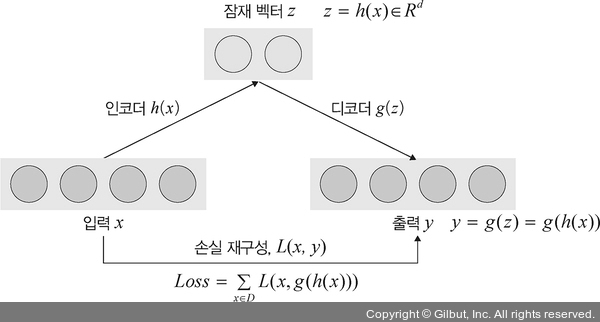
▲ 그림 13-4 오토인코더의 인코더와 디코더