1. 샘플링한 z를 디코더 네트워크 p_θ(x|z)에 보내 (μ_z|x, Σ_z|x)를 출력한 후 이를 이용하여 ①항의 값을 구합니다(다음 수식은 앞의 수식과 동일합니다).

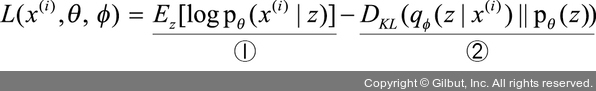
2. (μ_x|z, Σ_x|z)의 가우시안 분포에서 z를 샘플링한 후 x'를 구합니다.

x' ← x|z ~ N(μ_x|z, Σ_x|z)

3. 역전파를 이용하여 L(x⁽ⁱ⁾, θ, ϕ)의 값이 높아지는 방향으로 기울기를 업데이트합니다. 즉, 가능도(likelihood)가 증가하는 방향으로 파라미터 θ와 ϕ를 업데이트합니다.

최종적으로 x와 유사한 x'라는 이미지가 생성됩니다.

다음은 인코더와 디코더에서 사용된 수식을 정리한 내용입니다.

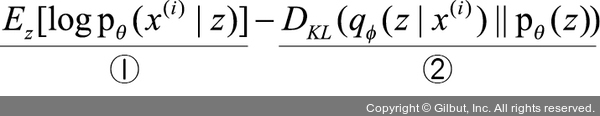
①항은 z가 주어졌을 때 x'를 표현하기 위한 확률밀도 함수로 디코더 네트워크를 나타냅니다. 즉, 디코더 네트워크의 가능도가 크면 클수록 θ가 그 데이터를 잘 표현한다고 해석할 수 있습니다. 따라서 ①항이 크면 클수록 모델 가능도가 커집니다.