이 절에서 단일층 신경망의 또 다른 종류인 적응형 선형 뉴런(ADAptive LInear NEuron, ADALINE)을 살펴보겠습니다. 버나드 위드로우(Bernard Widrow)와 그의 박사 과정 학생인 테드 호프(Tedd Hoff)가 프랑크 로젠블라트의 퍼셉트론 알고리즘 이후 채 몇 년이 지나지 않아 아달린(Adaline)을 발표했습니다.¹⁶ 아달린은 퍼셉트론의 향상된 버전으로 볼 수 있습니다.

아달린은 연속 함수(continuous function)로 손실 함수를 정의하고 최소화하는 핵심 개념을 보여 주기 때문에 아주 흥미롭습니다. 이어지는 장에서 설명할 로지스틱 회귀(logistic regression), 서포트 벡터 머신(support vector machine), 다층 신경망(multilayer neural network) 같은 분류를 위한 다른 머신 러닝 모델과 선형 회귀 모델을 이해하는 데 도움이 될 것입니다.

아달린 규칙(위드로우-호프 규칙이라고도 함)과 로젠블라트 퍼셉트론의 가장 큰 차이점은 가중치를 업데이트하는 데 퍼셉트론처럼 단위 계단 함수 대신 선형 활성화 함수를 사용하는 것입니다. 아달린에서 선형 활성화 함수 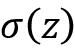는 단순한 항등 함수(identity function)입니다. 즉, 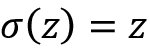입니다.

선형 활성화 함수가 가중치 학습에 사용되지만 최종 예측을 만들기 위해서는 여전히 임계 함수를 사용합니다. 앞서 보았던 단위 계단 함수와 비슷합니다.