2.3.1 경사 하강법으로 손실 함수 최소화

지도 학습 알고리즘의 핵심 구성 요소 중 하나는 학습 과정 동안 최적화하기 위해 정의한 목적 함수(object function)입니다. 종종 최소화하려는 손실 함수 또는 비용 함수가 목적 함수가 됩니다. 아달린은 계산된 출력과 진짜 클래스 레이블 사이의 평균 제곱 오차(Mean Squared Error, MSE)로 모델 파라미터¹⁷를 학습하기 위한 손실 함수 L을 정의합니다.

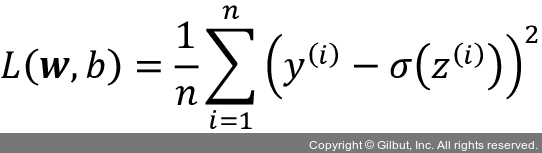
단위 계단 함수 대신 연속적인 선형 활성화 함수를 사용하는 장점은 손실 함수가 미분 가능해진다는 것입니다. 이 손실 함수의 또 다른 장점은 볼록 함수라는 것입니다. 간단하지만 강력한 최적화 알고리즘인 경사 하강법(gradient descent)을 적용하여 붓꽃 데이터셋의 샘플을 분류하도록 손실 함수를 최소화하는 가중치를 찾을 수 있습니다.

그림 2-10에서는 경사 하강법 이면에 있는 핵심 아이디어를 지역 또는 전역 최솟값에 도달할 때까지 언덕을 내려오는 것으로 묘사하고 있습니다. 각 반복에서 경사의 반대 방향으로 진행합니다. 진행 크기는 경사의 기울기와 학습률로 결정합니다(간단하게 그리기 위해 그림 2-10은 하나의 가중치 w만 나타냈습니다).