17세기 뉴턴이 미적분학(calculus)을 발견한 이후 수학의 황금 시대가 되었는데, 이때부터 이론 수학(abstract mathematics)의 시대라고 본다. 그 당시 집합(sets)과 논리(logic)가 중시되었다. 철학자로 유명한 러셀(Russell), 화이트헤드(Whitehead) 등도 이론 수학의 이론적 근거를 제공하였으며, 점차적으로 힐베르트(Hilbert), 괴델(Godel), 브라우어르(Brouwer) 등에 의해 더 발전하였다. 이 과정에서 집합 이론이 특히 발전하였는데 집합 이론은 숫자, 벡터, 함수 등을 표현하면서 정의를 도입하고 서로 간의 관계를 연구하였다. 이 과정에서 정리(theorem), 보조정리(lemma), 따름정리(corollary) 등이 도입되었다. 이론 수학이 발전하면서 수학자들은 자신의 문제를 좀 더 간결하게 표현하고, 해결할 수 있게 되었으며 이는 많은 성과로 이어졌다.

그 후, 수집된 데이터에 대한 수학적 접근이 본격적으로 이뤄지는 통계적 방법이 빠른 속도로 발전하기 시작했다. 결국 데이터 과학은 ‘숫자’를 다루는 분야이므로, 수학적 접근은 데이터를 바탕으로 문제를 정의하고 논리적으로 해결하는 데 큰 역할을 한다. 다양한 분야가 맞물려 돌아가는 데이터 과학에서 특히 가장 중요한 세 가지는 수학적 접근의 기반이 되는 ‘수학’과 데이터를 요약하고 파악하게 하는 ‘통계’, 불확실한 현상을 표현할 수 있는 ‘확률’일 것이다.

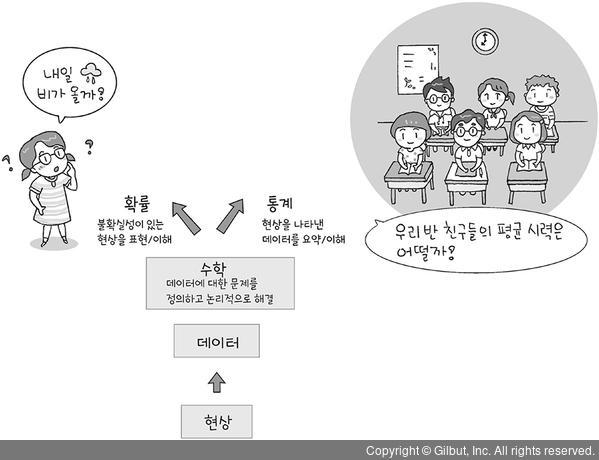
▲ 그림 1-21 데이터 과학에서의 수학적 접근