2.6.1 분석모형 응용 - 주성분 분석
이제 고윳값과 고유 벡터가 널리 활용되는 분야를 살펴보자. 살펴본 바와 같이 고윳값과 고유 벡터는 어떤 행렬이 갖는 특징이다. 바꿔 말하면, 어떤 행렬을 대표하는 고유한 값이라고 이해할 수 있다. 그럼 어떤 행렬 대신 고윳값과 고유 벡터를 통해 그 행렬을 ‘대신’할 수도 있을 것이다. 그냥 ‘대신’하는 것이 아니라 분해를 통해 좀 더 단순한 형태로, 하지만 원래 행렬의 특징은 더 잘 드러나게 표현할 수 있다. 그래서 고윳값과 고유 벡터는 크기가 큰 행렬(많은 변수를 갖는 어떤 데이터셋의 공분산행렬 또는 상관관계행렬)을 나타낼 때 해당 데이터셋의 변수 크기를 줄여주는 역할을 하며, 이를 차원 축소(dimension reduction)라 한다. 그리고 이러한 기법의 이름을 주성분 분석(principal component analysis)이라고 한다.
예를 들면 그림 2-15와 같이 변수 세 개로 표현된 점 열 한 개가 있다고 하자. 이 점들은 변수 세 개로 설명이 되지만, 더 잘 설명할 수 있는 두 개의 관점(주성분)을 찾아 그 관점으로 설명한다면 점 열 한 개의 특성을 더 잘 나타날 수 있다.

▲ 그림 2-15 주성분 분석을 통한 주성분 1과 2의 발견
Note ≡
앞서 자료 구조에서 살펴본 ‘차원’과 이 절에서 얘기하는 ‘차원’의 성격은 다르다. 앞서 파이썬 자료 구조 부분에서 살펴본 ‘차원’은 자료 형태를 나타냈는데, 예를 들어 2차원이면 행과 열이 있는 자료 구조였다. 반면에 여기서의 ‘차원’은 변수의 개수를 나타내고, ‘차원’의 감소는 분석 시 사용하는 변수 개수의 감소를 의미한다. 이런 맥락에서 차원의 저주(curse of dimensionality)라는 표현도 간혹 볼 수 있는데, 변수가 많으면 분석 모델링에 어려운 점이 늘어나는 것을 의미한다.
주성분 분석은 기본적으로 고윳값과 고유 벡터를 활용하여 자료(행렬)를 다르게 표현하는 방법인데, 특히 행렬에서 열에 해당하는 변수를 주성분으로 대신할 수 있다. 주성분 분석에 대한 너무 상세한 내용이나 수식보다는 우선 직관적으로 이해해보자. 앞에서 살펴본 것처럼 변수들은 각 특성을 나타내다 보니 사실 서로 관련이 없어야 하지만, 현실에서는 상관관계가 어느 정도 존재한다. 일반적으로 변수들이 서로 상관관계가 없다면 좀 더 효과적으로 데이터를 분석할 수 있다. 그래서 주성분은 기존 변수의 선형 변환을 통해 상관관계가 적은 새로 만들어진 변수를 의미한다.
여기서의 선형 변환이라는 것은 기존 변수를 나타낸 데이터를 다음과 같은 변수에 어떤 값을 곱하고 더하여 일차식으로 변환해서 새로운 값을 얻는 것을 의미한다.
주성분 = 계수 × 원데이터(raw data) + 절편
즉, 원데이터에 한 숫자를 곱하고, 또 다른 숫자를 더해서 새로운 값으로 만드는 것이 바로 주성분이 된다. 주성분은 최대로 원래 변수의 개수만큼 만들 수 있다. 그런데 첫 번째 주성분부터 원데이터를 최대한 잘 표현해 만들다 보니, 마지막에 만드는 주성분은 별로 영양가가 없을 수 있다. 그러므로 주성분 분석에서 주성분은 변수의 개수보다 적게 사용한다.
어떻게 해서 주성분 사이에서 선형적인 관계가 안 나오는 것일까? 선형 관계란 한 변수가 커질 때 다른 변수도 커지거나 작아지는 관계이다. 그런데 인위적으로 주성분들은 서로 수직이 되도록 생성되어 선형적인 상관관계가 없는 것이며, 기존 변수(행렬의 열에 해당하는)가 주성분에 의해 행렬에서 새로운 좌표로 표현된다. 특히, 자료의 분산이 잘 표현되니 원래 행렬이 갖는 분산을 잘 나타내게 된다. 즉, 주어진 데이터의 변수보다 적은 수의 주성분으로 주어진 데이터를 최대한 많이 표현한다.
여기서 한 가지 궁금한 점은 자료를 잘 나타낸다는 것이 자료의 정보를 많이 표현한다는 것과 같은 의미냐라는 것이다. 사실 정보라는 것은 한 가지 고정된 어떤 값에서 변화가 없다면 굳이 그 정보를 알 필요도 없고 정보의 가치도 없게 된다. 즉, 각 값이 중심에서 어느 정도 떨어져서 변동이 있어야 우리는 그 데이터를 통해 분석할 이유가 있는 것이다. 이러한 변동을 우리는 일반적으로 자료가 갖는 정보로 이해할 수 있다. 원데이터의 변수도 이러한 정보를 나타내지만, 주성분은 이러한 정보를 더 잘 나타낸다. 그것도 분산을 더 잘 나타내는 주성분을 찾을 수 있다.
다음 그림을 통해서 주성분이 어떻게 구해지는지 살펴보자.
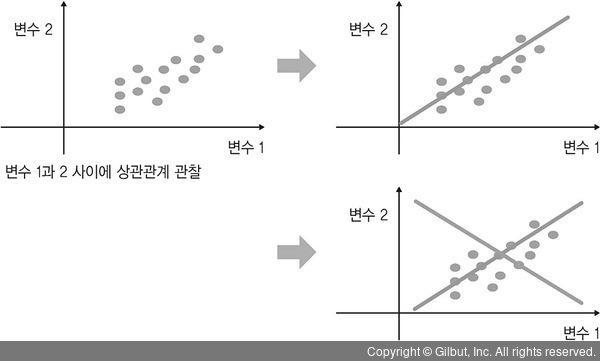
▲ 그림 2-16 주성분 발견 과정
예를 들어 변수가 두 개인 데이터(열이 두 개인 행렬)가 있다고 하자. 이 데이터들은 그림 2-16과 같이 회색 점으로 분포되어 있다. 변수 간의 관계를 살펴보니 변수 1과 2는 선형적인 상관관계가 존재한다. 그렇다면 주성분을 통해 상관관계가 없는 새로운 두 변수를 만들어 보자.
우선 첫 번째 주성분은 데이터의 정보를 가장 잘 표현하는 축을 찾아준다. 그림 2-16에서는 데이터를 가장 잘 나타내는 주황색 직선이 된다. 첫 번째 주성분 위의 좌표로 각 점들을 표현할 수 있다. 그리고 주황색 직선은 변수 1과 2의 선형식으로 나타낼 수 있다. 이제 두 번째 주성분을 찾아보자.
우리가 공들여 찾은 첫 번째 주성분과 선형 관계가 없어야 하니 첫 번째 주성분에 수직인 직선을 찾아야 한다. 회색 직선이 하는 역할은 주황색 직선에 의해 미처 설명되지 못했던 데이터의 정보를 설명하는 것이다. 그리고 데이터들은 두 번째 주성분 위의 좌표로 표현된다.
다음 코드에서는 원래 주어진 변수 세 개로 표현되는 데이터를 주성분 분석하며, 결과 중 1열과 2열이 바로 주성분 1과 주성분 2에 해당된다(당연히 3열은 주성분 3이 된다.)
# sklearn 패키지 decomposition 모듈의 PCA 함수 불러오기 >>> from sklearn.decomposition import PCA >>> M = np.array( [[-1, -1, -1], [-2, -1, 2], [-3, -2, 0], [1, 1, 2], [2, 1, 1], [3, 2, 4], [2, 0, 3], [3, 5, 1], [4, 2, 3], [3, 3, 2]] ) # 원래 데이터 >>> pca = PCA(n_components=2) # 주성분을 두 개로 지정 # 주성분 분석 >>> pca.fit(M) PCA(copy=True, iterated_power='auto', n_components=2, random_state=None, svd_solver='auto', tol=0.0, whiten=False) >>> PC = pca.transform(M) # w는 고윳값, V는 고유 벡터 >>> w, V = np.linalg.eig(pca.get_covariance()) # 원래 데이터를 나타내는 주성분 세 개 >>> V.T.dot(M.T).T array([[-1.63789386, 0.38309423, -0.41296792], [-1.50265209, -1.67967793, 1.98008049], [-3.43143719, -0.83088857, 0.73134327], [ 1.9287851 , -0.84878936, 1.24873722], [ 2.3753258 , 0.28259255, 0.52722744], [ 4.59500215, -1.03189193, 2.61173397], [ 2.3475376 , -0.06571181, 2.73582697], [ 5.55104049, -1.38406422, -1.5067567 ], [ 5.04154285, 0.09948998, 1.89022418], [ 4.62279035, -0.68358757, 0.40313444]])
지금까지 살펴본 것처럼 자료를 행렬로 표현하면 선행대수를 활용할 수 있어 데이터 분석을 더 효율적으로 할 수 있다. 다음 절에서 실습을 통해 다양한 내용을 연습해보자.