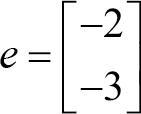이제 두 벡터의 합을 수식으로 표현해보자.

같은 위치, 즉 같은 차원에 해당하는 원소를 더한 결과를 기존 벡터와 같은 차원의 벡터로 새롭게 표시하기만 하면 된다. 직관적으로는 두 어린이의 힘을 나타내는 화살표를 이어준 것이, 즉 수치적으로는 같은 차원의 원소를 더한 것이 바로 벡터의 합이다.

>>> import numpy as np
>>> c = np.array([2, 3])
>>> d = np.array([1, 3])
>>> c + d
array([3, 6])

이번에는 앞의 두 벡터 중에서 벡터 c를 좀 더 살펴보자. 예를 들어 어떤 힘을 나타내는 벡터 c가 두 배가 된다는 것은 어떤 의미일까? 벡터 c가 두 배가 된다는 것은 같은 방향으로 힘의 세기가 두 배 된다는 것을 의미한다. 만약 벡터 c와 힘의 크기는 같지만, 방향만 반대인 벡터는 어떻게 표현할까? 그 벡터는 같은 길이이지만 방향이 반대인 화살표를 생각할 수 있다. 이 ‘반대 방향 화살표’를 수치적으로 나타내기 위해 기존 벡터에 -1을 곱해보자. 벡터 c에 1을 곱하면 c는 변하지 않는다. 변하지 않는다는 의미는 크기와 방향이 변하지 않음을 의미한다. -1을 곱한다면 크기는 변하지 않지만, 방향은 반대가 된다. 이때 곱하는 값은 숫자이고, 곱하는 벡터는 여러 숫자로 구성된 벡터이다. 곱하는 숫자를 ‘스칼라’라고 부르며, 벡터와 스칼라의 곱은 이처럼 벡터의 방향과 세기를 변화시킨다. 벡터 c에 -1을 곱한 벡터 e는 다음과 같다.