행렬의 종류

행렬은 행과 열로 표현된 여러 수치의 모음이지만, 어떤 숫자들이 어떻게 표현되는지에 따라서, 즉 원소에 어떤 숫자가 어떻게 배치되는가에 따라 여러 종류로 분류할 수 있다. 행렬 중에서도 원소의 값이 모두 0인 행렬을 영행렬(zero matrix)이라 한다.

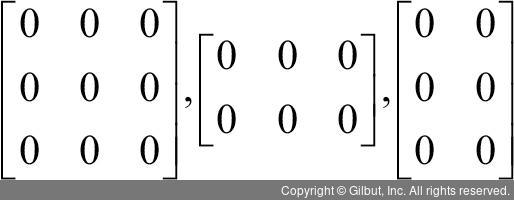
앞에서 다양한 영행렬을 제시하였는데, 이 중에 행과 열의 크기가 다르기도 하고 같기도 하다. 행과 열의 크기가 같은 행렬을 정방행렬(square matrix)이라고 한다. 정방행렬에서 대각선에 해당되는 곳(대각 성분)만 0이 아니고, 나머지(비대각 성분) 원소의 값이 0인 경우가 있는데 이런 행렬은 대각행렬(diagonal matrix)이라 한다.

굳이 0인 비대각 성분을 다 표현하는 것은 그다지 효율적인 방법이 아닐 수 있다. 그래서 대각행렬은 다음과 같이 표현하기도 한다.

대각행렬은 행렬의 대각선에서 여러 값의 조합으로 구성될 수 있고, 그중에서도 값이 1로만 구성된 행렬을 항등행렬(identity matrix)이라 부른다. 다음은 3행 3열짜리 항등행렬이다.

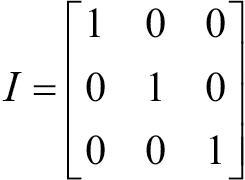
대각행렬, 항등행렬 모두 행렬의 대각선 위에만 값이 존재한다. 다음 절에서 살펴보겠지만 행렬의 대각선은 행렬을 다루는 데 있어 중요한 역할을 한다. 대각은 행렬을 연산할 때 많이 활용된다.

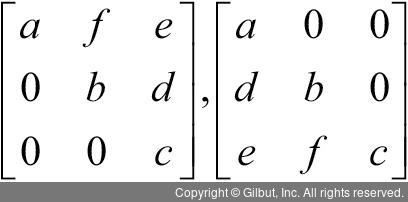
그 외에도 대각선을 기준으로 위 쪽에만 원소 값이 있는 상삼각행렬(upper triangular matrix), 대각선을 기준으로 아래 쪽에만 원소 값이 있는 하삼각행렬(lower triangular matrix) 등이 있다(왼쪽이 상삼각행렬, 오른쪽이 하삼각행렬).